题目内容
【题目】如图,已知反比例函数![]() 的图象经过点A(﹣1,a),过点A作AB⊥x轴,垂足为点B,△AOB的面积为
的图象经过点A(﹣1,a),过点A作AB⊥x轴,垂足为点B,△AOB的面积为![]() .
.
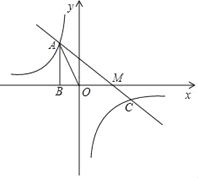
(1)求k的值;
(2)若一次函数y=mx+n图象经过点A和反比例函数图象上另一点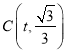 ,且与x轴交于M点,求AM的值;
,且与x轴交于M点,求AM的值;
(3)在(2)的条件下,如果以线段AM为一边作等边△AMN,顶点N在另一个反比例函数![]() 上,则k'= .
上,则k'= .
【答案】(1)![]() ;(2)
;(2)![]() ;(3):4
;(3):4![]() 或
或![]() .
.
【解析】
(1)根据点A的坐标以及三角形的面积公式即可求出a值,再根据反比例函数图象上点的坐标特征即可求出k的值;
(2)根据反比例函数解析式可求出点C的坐标,由点A、C的坐标利用待定系数法即可求出直线AM的解析式,令直线AM的解析式中y=0求出x值,即可得出点M的坐标,再利用勾股定理即可求出线段AM的长度;
(3)设点N的坐标为(m,n),由等边三角形的性质结合三角函数找出关于m、n的关系来求得点N.
解:(1)∵S△AOB=![]() OBAB=
OBAB=![]() ,
,
∴![]() ×1×a=
×1×a=![]() ,
,
∴a=![]() .
.
∴点A(﹣1,![]() ).
).
∵反比例函数y=![]() 的图象经过点A (﹣1,
的图象经过点A (﹣1,![]() ),
),
∴k=﹣![]() .
.
(2)∵C (t,![]() )在反比例函数y=
)在反比例函数y=![]() 的图象上,
的图象上,
∴![]() t=﹣
t=﹣![]() ,解得:t=3,
,解得:t=3,
∴C(3,![]() ).
).
将A(﹣1,![]() )、C(3,
)、C(3,![]() )代入y=mx+n中,
)代入y=mx+n中,
得:![]() ,解得:
,解得: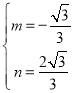 ,
,
∴直线AM的解析式为y=![]() x+
x+![]() .
.
令y=![]() x+
x+![]() 中y=0,则x=2,
中y=0,则x=2,
∴M(2,0).
在Rt△ABM中,AB=![]() ,BM=2﹣(﹣1)=3,
,BM=2﹣(﹣1)=3,
∴AM=![]() =2
=2![]() .
.
(3)设点N的坐标为(m,n),
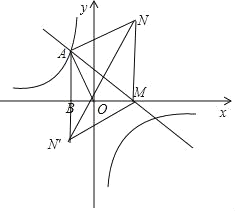
∵△AMN为等边三角形,且AM=2![]() .
.
∴∠AMN=60°,
∵tan∠AMB=![]() =
=![]() ,
,
∴∠AMB=30°,
∴∠NMB=90°,
∴N(2,2![]() ),
),
同法可得:当△AMN′是等边三角形时,可得N′(﹣1,﹣![]() ),
),
∵顶点N在另一个反比例函数y=![]() 上,
上,
∴k′=4![]() 或
或![]()
故答案为:4![]() 或
或![]() .
.

练习册系列答案
相关题目