Question

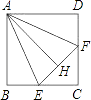
【题目】如图，在正方形ABCD中，点E、F分别在BC、CD上移动，但A到EF的距离AH始终保持与AB长相等，问在E、F移动过程中：
（1）∠EAF的大小是否有变化？请说明理由．
（2）△ECF的周长是否有变化？请说明理由．

Answer 1

【答案】
（1）解：∠EAF的大小没有变化．理由如下：

根据题意，知

AB=AH，∠B=90°，

又∵AH⊥EF，

∴∠AHE=90°，

∵AE=AE，

∴Rt△BAE≌Rt△HAE（HL），

∴∠BAE=∠HAE，

同理，△HAF≌△DAF，

∴∠HAF=∠DAF，

∴∠EAF=∠EAH+∠FAH= ∠BAH+ ∠HAD= （∠BAH+∠HAD）= ∠BAD，

又∵∠BAD=90°，

∴∠EAF=45°，

∴∠EAF的大小没有变化．

（2）解：△ECF的周长没有变化．理由如下：

∵由（1）知，Rt△BAE≌Rt△HAE，△HAF≌△DAF，

∴BE=HE，HF=DF，

∴C△EFC=EF+EC+FC=EB+DF+EC+FC=2BC，

∴△ECF的周长没有变化．

【解析】（1）根据题意，求证△BAE≌△HAE，△HAF≌△DAF，然后根据全等三角形的性质求∠EAF= ∠BAD．（2）根据（1）的求证结果，用等量代换来计算△ECF的周长，如果结果是定量，就说明△ECF的周长没有变化，反之，△ECF的周长有变化．
【考点精析】解答此题的关键在于理解正方形的性质的相关知识，掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．