题目内容
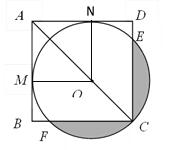
【题目】如图,O为正方形ABCD的对角线AC上一点,以O为圆心,OC的长为半径的![]() 与AB相切于点M.
与AB相切于点M.
![]() 求证:AD与
求证:AD与![]() 相切;
相切;
![]() 若
若![]() ,求图中阴影部分面积.
,求图中阴影部分面积.
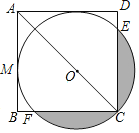
【答案】(1)见解析;(2)2π-4.
【解析】
(1)过O作ON⊥AD于N,由垂直的定义得到∠ONA=90°,根据正方形的性质得到∠OAN=∠OAM=45°,根据切线的性质得到∠OMA=90°,根据全等三角形的性质得到ON=OM,于是得到结论;
(2)首先求出AE=AF,进而求出△CEF的面积,进而得出阴影部分的面积.
解: (1)证明:连接OM,过O作ON⊥AD于N,
∴∠ONA=90°,
∵四边形ABCD是正方形,
∴∠OAN=∠OAM =45°,
∵AB与⊙O相切于M,
∴∠OMA=90°,
在△ONA与△OMA中,
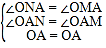 ,
,
∴△ONA≌△OMA,
∴ON=OM,
∴BC与⊙O相切;
(2)设⊙O的半径为r.
显然OM∥CB,
∴△AOM∽△ACB,
∴ ![]() ,即
,即![]() ,
,

解得r=2
故⊙O的半径为2;
连接EF,

则EF是⊙O的直径,
∵AC是正方形ABCD的对角线,
∴∠DAC=45°,
∵CO=FO,
∴∠CFO=45°,
∴∠COF=90°,
则AE=AF,
∵EF=4,
∴CE=CF=2![]() ,
,
∴S△CEF=![]() ×2
×2![]() ×2
×2![]() =4,
=4,![]() =
=![]() =
=![]() ,
,
故阴影部分面积: ![]() -4.
-4.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目