题目内容
【题目】将横截面为等腰三角形ABC的物体按如图29-Z-25所示放在水平地面上,AB=AC=2,∠BAC=120°,边AB紧贴地面.有一光源S,在其照射下,该物体的影子AD=6,将△ABC绕点A旋转60°后,点C落在地面上的点C′处,点B转至点B′处,此时B′的影子恰好落在C′处.
(1)试在图中画出光源S所在的位置;
(2)求出光源S到地面的距离.
![]()
【答案】(1)见解析;(2)光源S到地面的距离为2![]()
【解析】
(1)根据题意画出图形;
(2)分别过点S,B′作地面的垂线,垂足分别为H、M、N,则AN=AM=1,设BH=y,SH=x,由相似三角形的判定定理可得出△CND∽△SHD,△B′MCC′∽△SHC′,根据相似三角形的对应边成比例求出x、y的值,进而得出结论.
(1)如图所示.

(2) 分别过点S,B′作地面的垂线,垂足分别为H、M、N,则AN=AM=1,
设BH=y,SH=x,
可证△CND∽△SHD,△B′MCC′∽△SHC′,
∴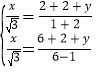 ,
,
∴![]() ,
,
∴S到地面的高度是2![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目