题目内容
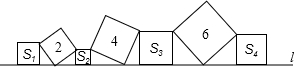
如图，在直线L上依次摆放着七个正方形，已知斜放置的三个正方形的面积分别为2，4，6，正放置的四个正方形的面积依次为s1，s2，s3，s4，则s1+s2+s3+s4=
8
8
．分析：如图，易证△ABC≌△CDE，得AB2+DE2=DE2+CD2=CE2，同理FG2+LK2=HL2，S1+S2+S3+S4=6+2=8．
解答：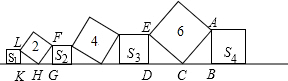
解：在△ABC和△CDE中，
∴△ABC≌△CDE（ASA），
∴AB=CD，BC=DE，
∴AB2+DE2=DE2+CD2=CE2=6，
同理可证FG2+LK2=HL2=2，
∴S1+S2+S3+S4=CE2+HL2=6+2=8．
故答案为：8．
解：在△ABC和△CDE中，
|
∴△ABC≌△CDE（ASA），
∴AB=CD，BC=DE，
∴AB2+DE2=DE2+CD2=CE2=6，
同理可证FG2+LK2=HL2=2，
∴S1+S2+S3+S4=CE2+HL2=6+2=8．
故答案为：8．
点评：本题考查了全等三角形的证明，考查了勾股定理的灵活运用，本题中证明AB2+DE2=DE2+CD2=CE2是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，在直线L上依次摆放着三个正方形，已知中间斜放置的正方形的面积是6，则正放置的两个正方形的面积之和为（ ）| A、6 | ||
| B、5 | ||
C、
| ||
| D、36 |
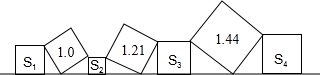正方形的面积分别为1.0，1.21，1.44，正放置的四个正方形的面积为S1、S2、S3、S4，则S1+S2+S3+S4=