题目内容
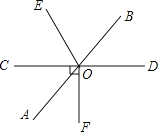
【题目】如图,直线AB,CD相交于点O,OE平分∠BOC,∠COF=90°.
(1)若∠BOE=65°,求∠AOF的度数;
(2)若∠BOD:∠BOE=1:2,求∠AOF的度数
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据角平分线的定义求出∠BOC的度数,根据邻补角的性质求出∠AOC的度数,根据余角的概念计算即可;
(2)根据角平分线的定义结合题意求出∠BOD,然后根据对顶角相等和余角的概念计算即可.
解:(1)∵OE平分∠BOC,∠BOE=65°,
∴∠BOC=2∠BOE=130°,
∴∠AOC=180°﹣130°=50°,
又∵∠COF=90°
∴∠AOF=90°﹣50°=40°;
(2)∵OE平分∠BOC,
∴∠BOD:∠BOE:∠EOC=1:2:2,
∴∠BOD=180°×![]() =36°,
=36°,
∴∠AOC=36°,
又∵∠COF=90°,
∴∠AOF=90°﹣36°=54°.

练习册系列答案
相关题目