题目内容
【题目】如图,函数![]() (k为常数,k>0)的图象与过原点的O的直线相交于A,B两点,点M是第一象限内双曲线上的动点(点M在点A的左侧),直线AM分别交x轴,y轴于C,D两点,连接BM分别交x轴,y轴于点E,F.现有以下四个结论:①△ODM与△OCA的面积相等;②若BM⊥AM于点M,则∠MBA=30°;③若M点的横坐标为1,△OAM为等边三角形,则
(k为常数,k>0)的图象与过原点的O的直线相交于A,B两点,点M是第一象限内双曲线上的动点(点M在点A的左侧),直线AM分别交x轴,y轴于C,D两点,连接BM分别交x轴,y轴于点E,F.现有以下四个结论:①△ODM与△OCA的面积相等;②若BM⊥AM于点M,则∠MBA=30°;③若M点的横坐标为1,△OAM为等边三角形,则![]() ;④若
;④若![]() ,则MD=2MA.其中正确的结论的序号是_______.
,则MD=2MA.其中正确的结论的序号是_______.

【答案】①③④
【解析】
①设点A(m,![]() ),M(n,
),M(n,![]() ),构建一次函数求出C,D坐标,利用三角形的面积公式计算即可判断.
),构建一次函数求出C,D坐标,利用三角形的面积公式计算即可判断.
②△OMA不一定是等边三角形,故结论不一定成立.
③设M(1,k),由△OAM为等边三角形,推出OA=OM=AM,可得1+k2=m2+![]() ,推出m=k,根据OM=AM,构建方程求出k即可判断.
,推出m=k,根据OM=AM,构建方程求出k即可判断.
④如图,作MK∥OD交OA于K.利用平行线分线段成比例定理解决问题即可.
①设点A(m,![]() ),M(n,
),M(n,![]() ),
),
则直线AC的解析式为y=-![]() x+
x+![]() +
+![]() ,
,
∴C(m+n,0),D(0,![]() ),
),
∴![]() ,
,
∴△ODM与△OCA的面积相等,故①正确;
∵反比例函数与正比例函数关于原点对称,
∴O是AB的中点,
∵BM⊥AM,
∴OM=OA,
∴k=mn,
∴A(m,n),M(n,m),
∴![]() ,
,
∴AM不一定等于OM,
∴∠BAM不一定是60°,
∴∠MBA不一定是30°.故②错误,
∵M点的横坐标为1,
∴可以假设M(1,k),
∵△OAM为等边三角形,
∴OA=OM=AM,
1+k2=m2+![]() ,
,
∵m>0,k>0,
∴m=k,
∵OM=AM,
∴(1-m)2+(k![]() )2=1+k2,
)2=1+k2,
∴k2-4k+1=0,
∴k=2±![]() ,
,
∵m>1,
∴k=2+![]() ,故③正确,
,故③正确,
如图,作MK∥OD交OA于K.
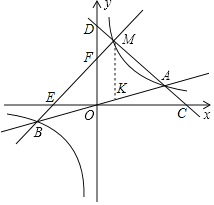
∵OF∥MK,
![]() ,
,
∴![]() ,
,
∵OA=OB,
∴![]() ,
,
∴![]() ,
,
∵KM∥OD,
∴![]() ,
,
∴DM=2AM,故④正确.
故答案为①③④.

 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案【题目】某校为了解七年级学生的体重情况,随机抽取了七年级m名学生进行调查,将抽取学生的体重情况绘制如下不完整的频数分布表和扇形统计图.
组别 | 体重(千克) | 人数 |
A | 37.5≤x<42.5 | 10 |
B | 42.5≤x<47.5 | n |
C | 47.5≤x<52.5 | 40 |
D | 52.5≤x<57.5 | 20 |
E | 57.5≤x<62.5 | 10 |

请根据图表信息回答下列问题:
(1)填空:①m=_____,②n=_____,③在扇形统计图中,C组所在扇形的圆心角的度数等于_______度;
(2)若把每组中各个体重值用这组数据的中间值代替(例如:A组数据中间值为40千克),则被调查学生的平均体重是多少千克?
(3)如果该校七年级有1000名学生,请估算七年级体重低于47.5千克的学生大约有多少人?