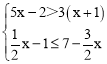题目内容
【题目】已知点O在直线MN上,过点O作射线OP,使∠MOP=130°,现将一块直角三角板的直角顶点始终放在点O处.

(1)如图①,当三角板的一边OA在射线OM上,另一边OB在直线MN的上方时,∠POB的度数 是 ;
(2)若将三角板绕点O旋转至图②所示的位置,此时OB恰好平分∠PON,则∠BOP 的度数为 ;∠AOM 的度数为 ;
(3)若将三角板绕点O旋转至图③所示位置,此时OA在∠PON 的内部,
①若 OP 所在的直线平分∠MOB,则∠POA 的度数为 ;
②∠BON-∠POA的度数为 .
【答案】(1)40゜;(2)25゜,65゜;(3)①40゜;②40゜.
【解析】
(1)根据∠POB=∠MOP-∠AOB代入数据即可求出结论;
(2)根据∠PON=180°-∠MOP可算出∠PON的度数,根据OB平分∠PON即可求出∠POB的度数,再通过角的计算可得出∠AOP=60°,结合∠MOP=130°即可得出∠AOM;
(3)①根据OP 所在的直线平分∠MOB,可得出∠MOB=100°,从而可求出∠BON=80°,根据∠BOA=90°求出∠AON=10°,根据∠POA=∠PON-∠AON可得结论;
②设∠AON=x°,则∠BON=90°-x°,∠POA=50°-x°,二者做差即可得出结论.
(1)∠POB=∠MOP-∠AOB=130°-90°=40°.
(2)∵∠MON是平角,∠MOP=130゜,
∴∠PON=∠MON-∠MOP=180゜-130゜=50゜
∵OB 平分∠PON,
∴∠BOP=![]() ∠PON=25゜
∠PON=25゜
∵∠AOB=90゜,
∴∠AOP=∠AOB-∠BOP=90゜-25゜=65゜
∴∠MOA=∠MOP-∠AOP=130゜-65゜=65゜;
(3)①如图,OE是PO的延长线,

∵∠MOP=130゜
∴∠MOE=50゜
∵OE是∠MOB的平分线,
∴∠MOB=100゜,
∴∠BON=80゜
∵∠AOB=90゜
∴∠AON=∠AOB-∠BON=90゜-80゜=10゜
∴∠POA=∠PON-∠AON=50゜-10゜=40゜;
②设∠AON=x°,则∠BON=90°-x°,∠POA=50°-x°,
∴∠BON-∠POA=(90°-x°)-(50°-x°)=40°.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案