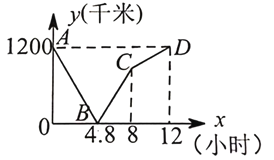题目内容
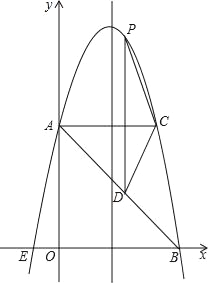
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E,B.
(1)求二次函数y=ax2+bx+c的解析式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积.
【答案】(1)y=﹣x2+4x+5(2)点P(![]() ,
, ![]() )时,S四边形APCD最大=
)时,S四边形APCD最大=![]()
【解析】(1)利用顶点式即可求出二次函数解析式;
(2)先求出直线AB的解析式,设出点P坐标(x,-x2+4x+5),建立函数关系式S四边形APCD=![]() ×AC×PD=2(-x2+5x)=-2x2+10x,根据二次函数求出极值即可.
×AC×PD=2(-x2+5x)=-2x2+10x,根据二次函数求出极值即可.
解:(1)设抛物线解析式为y=a(x﹣2)2+9,
∵抛物线与y轴交于点A(0,5),
∴4a+9=5,
∴a=﹣1,
y=﹣(x﹣2)2+9=﹣x2+4x+5,
(2)当y=0时,﹣x2+4x+5=0,
∴x1=﹣1,x2=5,
∴E(﹣1,0),B(5,0),
设直线AB的解析式为y=mx+n,
∵A(0,5),B(5,0),
∴m=﹣1,n=5,
∴直线AB的解析式为y=﹣x+5;
设P(x,﹣x2+4x+5),
∴D(x,﹣x+5),
∴PD=﹣x2+4x+5+x﹣5=﹣x2+5x,
∵AC=4,
∴S四边形APCD=![]() ×AC×PD=2(﹣x2+5x)=﹣2x2+10x=﹣(x﹣
×AC×PD=2(﹣x2+5x)=﹣2x2+10x=﹣(x﹣![]() )2+
)2+![]() ,
,
∵﹣1<0
∴当x=![]() 时,
时,
∴即:点P(![]() ,
, ![]() )时,S四边形APCD最大=
)时,S四边形APCD最大=![]() .
.

【题目】为了加强市民的节水意识,合理利用水资源,某市采用阶梯收费的调控手段以达到节水的目的,该市自来水收费价目表如下:
每月用水量 | 价格 | 注:水费按月结算,每户每月须缴纳5元污水处理费. |
不超出6m3的部分 | 2元/m3 | |
超出6m3不超出10m3的部分 | 3元/m3 | |
超出10m3的部分 | 5元/m3 |
若某户居民![]() 月份用水
月份用水![]() ,则应缴费
,则应缴费![]() (元),
(元),
(1)若用户![]() 月份共用水
月份共用水![]() ,则需缴费________;
,则需缴费________;
(2)若该户居民某月缴费![]() 元,则该户居民该月用水多少吨?
元,则该户居民该月用水多少吨?