Question

【题目】如图，在平面直角坐标系中，O为坐标原点，四边形OABC是长方形，点A、C的坐标分别为A（10，0 ），C（0，4），点D是OA的中点，点P在BC边上运动，当△ODP是腰长为5的等腰三角形时，点P的坐标为（ ）

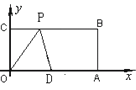
A. （3，4），（2，4） B. （3，4），（2，4），（8，4）

C. （2，4），（8，4） D. （3，4），（2，4），（8，4），（2.5，4）

Answer 1

【答案】B

【解析】试题解析：有两种情况：①以O为圆心，以5为半径画弧交BC于P点，此时OP=OD=5，

在Rt△OPC中，OC=4，OP=5，

由勾股定理得PC=3，

则P的坐标是（3，4）；

②以D为圆心，以5为半径画弧交BC于P′和P″点，此时DP′=DP″=OD=5，

过P′作P′N⊥OA于N，

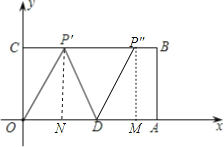
在Rt△OP′N中，设CP′=x，

则DN=5-x，P′N=4，OP=5，由勾股定理得：42+（5-x）2=52，

x=2，

则P′的坐标是（2，4）；

过P″作P″M⊥OA于M，

设BP″=a，

则DM=5-a，P″M=4，DP″=5，

在Rt△DP″M中，由勾股定理得：（5-a）2+42=52，

解得：a=2，

∴BP″=2，CP″=10-2=8，

即P″的坐标是（8，4）；

假设0P=PD，则由P点向0D边作垂线，交点为Q则有PQ2十QD2=PD2，

∵0P=PD=5=0D，

∴此时的△0PD为正三角形，于是PQ=4，QD=0D=2.5，PD=5，代入①式，等式不成立．所以排除此种可能．

故选B．