题目内容
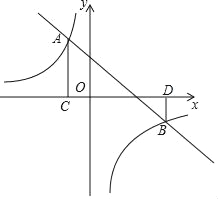
【题目】反比例函数![]() (
(![]() 为常数.且
为常数.且![]() )的图象经过点
)的图象经过点![]() .
.![]() .
.
(1)求反比例函数的解析式及![]() 点的坐标;
点的坐标;
(2)在![]() 轴上找一点
轴上找一点![]() .使
.使![]() 的值最小,
的值最小,
①求满足条件的点![]() 的坐标;②求
的坐标;②求![]() 的面积.
的面积.
【答案】(1)![]() ,B点坐标为(3,1);(2)①P点坐标为(
,B点坐标为(3,1);(2)①P点坐标为(![]() ,0);②
,0);②![]()
【解析】
(1)先把A点坐标代入![]() 求出k得到反比例函数解析式;然后把B(3,m)代入反比例函数解析式求出m得到B点坐标;
求出k得到反比例函数解析式;然后把B(3,m)代入反比例函数解析式求出m得到B点坐标;
(2)①作A点关于x轴的对称点A′,连接BA′交x轴于P点,则A′(1,-3),利用两点之间线段最短可判断此时PA+PB的值最小,再利用待定系数法求出直线BA′的解析式,然后求出直线与x轴的交点坐标即可得到P点坐标;
②根据![]() 的面积=梯形ABDC的面积-△PAC的面积-△PBD的面积计算即可.
的面积=梯形ABDC的面积-△PAC的面积-△PBD的面积计算即可.
解:(1)把A(1,3)代入![]() 得k=1×3=3,
得k=1×3=3,
∴反比例函数解析式为![]() ;
;
把B(3,m)代入![]() 得3m=3,解得m=1,
得3m=3,解得m=1,
∴B点坐标为(3,1);
(2)①作A点关于x轴的对称点A′,连接BA′交x轴于P点,则A′(1,-3),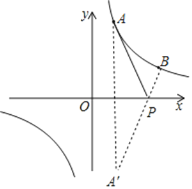
∵PA+PB=PA′+PB=BA′,
∴此时PA+PB的值最小,
设直线BA′的解析式为y=mx+n,
把A′(1,-3),B(3,1)代入得![]() ,解得
,解得![]() ,
,
∴直线BA′的解析式为y=2x-5,
当y=0时,2x-5=0,解得x=![]() ,
,
∴P点坐标为(![]() ,0);
,0);
②如图,连接AB,作BD⊥x轴于点D,设A A′与x轴交于点C,
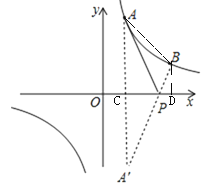
∵A(1,3),B(3,1),P(![]() ,0),
,0),
∴AC=3,BD=1,CD=2,CP=![]() ,PD=
,PD=![]() ,
,
∴![]() 的面积=梯形ABDC的面积-△PAC的面积-△PBD的面积
的面积=梯形ABDC的面积-△PAC的面积-△PBD的面积
=![]()
=![]()
=![]() .
.

练习册系列答案
相关题目