题目内容
 (2000•吉林)如图,⊙O的外切梯形ABCD中,若AD∥BC,那么∠DOC的度数为( )
(2000•吉林)如图,⊙O的外切梯形ABCD中,若AD∥BC,那么∠DOC的度数为( )A.70°
B.90°
C.60°
D.45°
【答案】分析:由于AD、DC、CB都是⊙O的切线,根据切线长定理知:∠ADO=∠CDO,∠DCO=∠BCO;而AD∥BC,则2∠ODC和2∠OCD互补,由此可求得∠DOC的度数.
解答:解:∵DA、CD、CB都与⊙O相切,
∴∠ADO=∠ODC,∠OCD=∠OCB;
∵AD∥BC,
∴∠ADC+∠BCD=180°;
∴∠ODC+∠OCD= (∠ADC+∠BCD)=
(∠ADC+∠BCD)= ×180°=90°,即∠DOC=90°;
×180°=90°,即∠DOC=90°;
故选B.
点评:此题主要考查的是切线长定理及平行线的性质.
解答:解:∵DA、CD、CB都与⊙O相切,
∴∠ADO=∠ODC,∠OCD=∠OCB;
∵AD∥BC,
∴∠ADC+∠BCD=180°;
∴∠ODC+∠OCD=
 (∠ADC+∠BCD)=
(∠ADC+∠BCD)= ×180°=90°,即∠DOC=90°;
×180°=90°,即∠DOC=90°;故选B.
点评:此题主要考查的是切线长定理及平行线的性质.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目

 ≈1.732)
≈1.732)

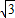 cm
cm cm
cm