题目内容
(2000•吉林)如图,一起重机的机身高21m,吊杆AB长36m,吊杆与水平线的夹角∠BAC可从30°升到80°.求起重机起吊的最大高度(吊钩本身的长度和所挂重物的高度忽略不计)和当起重机位置不变时使用的最大水平距离(精确到0.1米,sin80°=0.9848,cos80°=0.1736, ≈1.732)
≈1.732)
【答案】分析:当起重机起吊的高度最大时,△ABC的∠BAC=80°;当起重机位置不变时水平距离最大时,∠BAC=30°,根据三角函数即可求解.
解答:解:在Rt△ABC中,当∠BAC=80°时,
BC=ABsin80°=36×0.9848≈35.5(米);
35.5+21=56.5m,
∴起重机起吊的最大高度是56.5m;
在Rt△ABC中,当∠BAC=30°时,
AC=AB•cos30°=36× ≈31.18米.
≈31.18米.
同理,当吊杆与水平线的夹角∠BAC=80°时,当起重机位置到吊杆的顶端的水平距离是:36•cos80°=36×0.1736≈6.25米.
则当起重机位置不变时使用的最大水平距离是:31.18-6.25≈24.9米.
点评:正确理解起重机起吊的高度最大,以及水平距离最大的条件是解决本题的关键.
解答:解:在Rt△ABC中,当∠BAC=80°时,
BC=ABsin80°=36×0.9848≈35.5(米);
35.5+21=56.5m,
∴起重机起吊的最大高度是56.5m;
在Rt△ABC中,当∠BAC=30°时,
AC=AB•cos30°=36×
 ≈31.18米.
≈31.18米.同理,当吊杆与水平线的夹角∠BAC=80°时,当起重机位置到吊杆的顶端的水平距离是:36•cos80°=36×0.1736≈6.25米.
则当起重机位置不变时使用的最大水平距离是:31.18-6.25≈24.9米.
点评:正确理解起重机起吊的高度最大,以及水平距离最大的条件是解决本题的关键.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案
相关题目




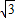 cm
cm cm
cm