Question

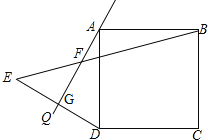
【题目】在小学，我们已经初步了解到，正方形的每个角都是90°，每条边都相等．如图，在正方形ABCD外侧作直线AQ，且∠QAD=30°，点D关于直线AQ的对称点为E，连接DE、BE，DE交AQ于点G，BE交AQ于点F．

（1）求∠ABE的度数；

（2）若AB=6，求FG的长．

Answer 1

【答案】（1）15°；（2）3

【解析】

试题分析：（1）连接AE，由轴对称的性质和线段垂直平分线的性质得出∠EAQ=∠QAD=30°，由正方形的性质得出∠BAD=90°，AB=AD，得出AE=AB，由等腰三角形的性质和三角形内角和定理即可得出结果；

（2）证出△AED是等边三角形，得出ED=6，由线段垂直平分线得出EG=3，∠FGE=90°，证出∠EFG=∠FEG=45°，得出EG=FG=3即可．

解：（1）连接AE，如图1所示：

∵点D关于直线AQ的对称点为E，

∴AE=AD，AQ垂直平分DE，

∴∠EAQ=∠QAD=30°，

∵四边形ABCD是正方形，

∴∠BAD=90°，AB=AD，

∴AE=AB，

∴∠BAE=30°+30°+90°=150°，

∴∠ABE=（180°﹣150°）=15°；

（2）由（1）得：AE=AD，∠EAD=60°，

∴△AED是等边三角形，ED=6，

∵AQ垂直平分DE，

∴EG=3，∠FGE=90°，

∵∠EAD=30°，∠AEB=15°，

∴∠EFG=∠FEG=45°，

∴EG=FG=3．