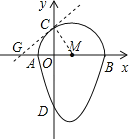��Ŀ����
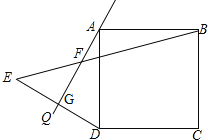
����Ŀ�����ǰ�һ����Բ����κ���ͼ���һ���ֺϳɵķ��ͼ�γ�Ϊ����Բ�������һ��ֱ���롰��Բ��ֻ��һ�����㣨��Բ����κ���ͼ������ӵ���⣩����ô����ֱ�߽�������Բ�������ߣ���ͼ�����κ���y=x2��2x��3��ͼ����x�ύ�ڵ�A��B����y�ύ�ڵ�D��ABΪ��Բֱ������ԲԲ��Ϊ��M����Բ��y��������ύ�ڵ�C��
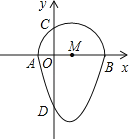
��1�����C�����ꣻ
��2���ֱ����������C�͵�D�ġ���Բ�������ߵı���ʽ��
���𰸡���1����0��![]() ������2��y=
������2��y=![]() x+
x+![]() ��y=��2x��3��
��y=��2x��3��
��������
�����������1������CM�������A��B�����꣬�����ɵõ�AB�ij�����Բ�İ뾶����������ɹ��ɶ��������OC�ij����̶��������C�����ꣻ
��2���ɣ�1����֪��C�����꣬�����C�ġ���Բ�������߽�x���ڵ�G��Ȼ������������������G�����꣬�ô���ϵ�������ֱ��GC�Ľ���ʽ����Ϊ������D�ġ���Բ�����߹�D�㣬���Ա���������Ľ���ʽΪy=kx��3������ͼ�����������ߵĽ���ʽ����Ϊ���У��������ǵĽ���ֻ��һ���������ɸ���һԪ���η��̵��й�֪ʶ������⣮
�⣺��1�������κ���y=x2��2x��3��ͼ����x�ύ�ڵ�A��B����y�ύ�ڵ�D��
����A����1��0������B�������ǣ�3��0����
��AB=4��
����ԲԲ��Ϊ��M��
��BM=AM=2��
��OM=1��
����CM��
��OC=![]() =
=![]() ��
��
����C�������ǣ�0��![]() ����
����
��2�������C�ġ���Բ�������߽�x���ڵ�G��
��GC����M�����ߣ�
���GCM=90����
��cos��OMC=![]() =
=![]() ��
��
��![]() =
=![]() ��
��
��MG=4��
��G����3��0����
��ֱ��GC�ı���ʽΪy=![]() x+
x+![]() ��
��
�����D��ֱ�߱���ʽΪy=kx��3��
��![]() ��
��
��x2����2+k��x=0��
���=[����2+k��]2=0��
��k=��2��
������D�ġ���Բ�������ߵı���ʽΪy=��2x��3��