题目内容
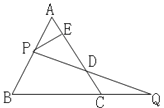
【题目】如图(图1)是由一副三角尺拼成的图案,其中三角尺AOB的边OB与三角尺OCD的边OD紧靠在一起.在图1中,∠AOC的度数是135°.

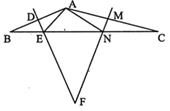
(1)固定三角尺AOB,把三角尺COD绕着点O旋转,当OB刚好是∠COD的平分线(如图2)时,∠AOC的度数是 ,∠AOC+∠OD= ;
(2)固定三角尺AOB,把三角尺COD绕点O旋转(如图3),在旋转过程中,如果保持OB在∠COB的内部,那么∠AOC+∠BOD的度数是否发生变化?请说明理由.
【答案】(1)112.5°,135°;
(2)∠AOC+∠BOD的度数不发生变化.理由见解析.
【解析】试题分析:(1)根据角平分线的定义得到∠COB=∠BOD=![]() ∠COD=22.5°,则∠AOC=∠AOB+∠COB=112.5°,于是可得到∠AOC+∠BOD=112.5°+22.5°=135°;(2)由于∠AOC=∠AOB+∠COB,则∠AOC+∠BOD=∠AOB+∠COB+∠BOD=∠AOB+∠COD=90°+45°=135°,所以∠AOC+∠BOD的度数不发生变化.
∠COD=22.5°,则∠AOC=∠AOB+∠COB=112.5°,于是可得到∠AOC+∠BOD=112.5°+22.5°=135°;(2)由于∠AOC=∠AOB+∠COB,则∠AOC+∠BOD=∠AOB+∠COB+∠BOD=∠AOB+∠COD=90°+45°=135°,所以∠AOC+∠BOD的度数不发生变化.
试题解析:(1)∵OB是∠COD的平分线,
∴∠COB=∠BOD=![]() ∠COD=22.5°,
∠COD=22.5°,
∴∠AOC=∠AOB+∠COB=112.5°,
∴∠AOC+∠BOD=112.5°+22.5°=135°.
故答案为112.5°,135°;
(2)∠AOC+∠BOD的度数不发生变化.理由如下:
∵∠AOC=∠AOB+∠COB,
∴∠AOC+∠BOD=∠AOB+∠COB+∠BOD=∠AOB+∠COD=90°+45°=135°,
∴∠AOC+∠BOD的度数不发生变化.

【题目】在一次中学生田径运动会上,参加跳高的15名运动员的成绩如下表所示:
成绩(m) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
人数 | 1 | 2 | 4 | 3 | 3 | 2 |
这15名运动员跳高成绩的中位数是( )
A. 4 B. 1.70 C. 1.75 D. 1.65