题目内容
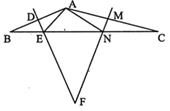
【题目】如图,在△ABC中,FD、FM分别是边AB、AC的垂直平分线,其垂足分别是D和M,交BC于点E、N,△BDE关于直线DF翻折后与△ADE重合,△CMN关于直线MF翻折后与△AMN重合.
(1)若BC的长为18厘米,求![]() AEN的周长;
AEN的周长;
(2)若∠F=40°,求∠BAC的度数.
【答案】(1)三角形AEN的周长为18厘米;(2)∠BAC=140°
【解析】试题分析:(1)由垂直平分线的性质可知BE=AE,AN=CN,由此 ![]() AEN周长为线段BC的长;(2)FD、FM分别是边AB、AC的垂直平分线,可得∠ADF=∠AMF=90°,由四边形内角和为360°,可得∠BAC的度数.
AEN周长为线段BC的长;(2)FD、FM分别是边AB、AC的垂直平分线,可得∠ADF=∠AMF=90°,由四边形内角和为360°,可得∠BAC的度数.
试题解析:(1)∵FD、FM分别是边AB、AC的垂直平分线,
∴BE=AE,AN=CN,
∴![]() AEN的周长=AE+EN+NM=BE+EN+NC=BC=18cm;
AEN的周长=AE+EN+NM=BE+EN+NC=BC=18cm;
(2)∵FD、FM分别是边AB、AC的垂直平分线,
∴∠ADF=∠AMF=90°,
∴∠BAC=360°-∠ADF-∠AMF-∠F=360°-90°-90°-40°=140°

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目