��Ŀ����
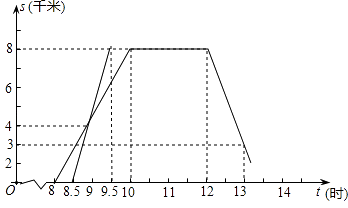
����Ŀ��ij��ʦ����ֲ֯���������8ʱ��ѧУ��������ֲ���ص�ֲ����ԭ·��У����ͼΪʦ����У·��s��ʱ��t֮���ͼ����ش��������⣺ 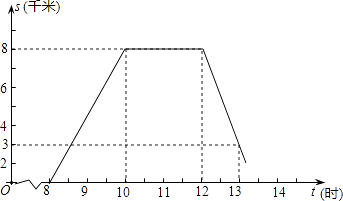
��1����ʦ����ʱ�ص�ѧУ��
��2�����������������ֳ���ʦ���ٰ�Сʱ��������ʦ��ͬ·����ǰ�������Сʱ����ֲ���ص㣬����ͼ�У����������ֳ���������ʱ����У·��s��ʱ��t֮���ͼ�����ͼ��ֱ��д�����ֳ���ʦ��ʱ����ѧУ��·�̣�
��3�����ʦ�������г�����8ʱ��������ֲ���ص��ֲ����2Сʱ��Ҫ��14ʱǰ���ص�ѧУ������ƽ���ٶȷֱ�Ϊÿʱ10km��8km������A��B��C��D�ĸ�ֲ������ѧУ��·�̷ֱ���13km��15km��17km��19km����ͨ������˵���ļ���ֲ�������Ҫ��
���𰸡�
��1���⣺��ʦ����Уʱ�ĺ�������ʽΪs=kt+b��
��ͼ��ʾ��
�ѣ�12��8������13��3��������ʽ�е� ![]() ��
��
��˷�����ã� ![]()
��s=��5t+68��
��s=0ʱ��t=13.6Сʱ��
��t=13ʱ36�֣�
��ʦ����13ʱ36�ֻص�ѧУ
��2���⣺�����ֳ���������ʱ����У·��s��ʱ��t֮���ͼ����ͼ��ʾ��
��ͼ��ã������ֳ���ʦ��ʱ����ѧУ4km
��3���⣺�����ѧУҪ���ֲ������ѧУ��·��Ϊx��km����
������ã� ![]() ��14����ã�x��
��14����ã�x�� ![]() ��
��
��A��B��C��D�ĸ�ֲ������ѧУ��·�̷ֱ���13km��15km��17km��19km��
��13�� ![]() ��15��
��15�� ![]() ��17��
��17�� ![]() ��19��
��19�� ![]() ��
��
��A��B��Cֲ�������ѧУ��Ҫ��
����������1���ȸ���ʦ����Уʱ��·����ʱ��֮��Ĺ�ϵ�г���������ʽ��Ȼ��ͼ�������Ӧs��t��ֵ����ɵõ�һ����Ԫһ�η����飬��˷�����ɵú�������ʽ��������ѧУʱ����sΪ0ʱ��t��ֵ����2����������ֱ�ӻ��������ֳ���������ʱ����У·��s��ʱ��t֮���ͼ��ͼ�ɵ����ֳ���ʦ��ʱ����ѧУ��·�̣���3���������ѧУҪ���ֲ������ѧУ��·��Ϊx��km����Ȼ�����������ƽ���ٶȡ�·�̺�ʱ��õ�һ������ʽ����˲���ʽ�ɵõ�x��ȡֵ��Χ����ȷ��ֲ�����Ƿ����Ҫ��

 ��һ������ĩ�ٷֳ�̾�ϵ�д�
��һ������ĩ�ٷֳ�̾�ϵ�д�����Ŀ����A����2��4��������ɵ�2��4�е����������ijһ��(��ijһ��)����֮��Ϊ��������ô�ı����(�����)���������ķ��ţ���Ϊһ������������
(1)���1��ʾ�����������������������ʹ�õ�������ÿ�еĸ���֮����ÿ�еĸ���֮�;�Ϊ�Ǹ���������д��ÿ���������������õ�������(д��һ�ַ�������)
1 | 2 | 3 | ��7 |
��2 | ��1 | 0 | 1 |
��1
(2)���2��ʾ������������һ�����������Ժ��ʹ�õ�������ÿ�еĸ���֮����ÿ�еĸ���֮�;�Ϊ�Ǹ�������������a��ֵ��
a | a2��1 | ��a | ��a2 |
2��a | 1��a2 | a��2 | a2 |
��2