题目内容
如图,下列图形都是由面积为1的正方形按一定的规律组成,其中,第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的正方形有5个,第(3)个图形中面积为1的正方形有9个,…,按此规律.则第(6)个图形中面积为1的正方形的个数为( )


| A、20 | B、27 | C、35 | D、40 |
考点:规律型:图形的变化类
专题:规律型
分析:第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的图象有2+3=5个,第(3)个图形中面积为1的正方形有2+3+4=9个,…,按此规律,第n个图形中面积为1的正方形有2+3+4+…+n=
,进一步求得第(6)个图形中面积为1的正方形的个数即可.
| n(n+3) |
| 2 |
解答:解:第(1)个图形中面积为1的正方形有2个,
第(2)个图形中面积为1的图象有2+3=5个,
第(3)个图形中面积为1的正方形有2+3+4=9个,
…,
按此规律,
第n个图形中面积为1的正方形有2+3+4+…+(n+1)=
个,
则第(6)个图形中面积为1的正方形的个数为2+3+4+5+6+7=27个.
故选:B.
第(2)个图形中面积为1的图象有2+3=5个,
第(3)个图形中面积为1的正方形有2+3+4=9个,
…,
按此规律,
第n个图形中面积为1的正方形有2+3+4+…+(n+1)=
| n(n+3) |
| 2 |
则第(6)个图形中面积为1的正方形的个数为2+3+4+5+6+7=27个.
故选:B.
点评:此题考查图形的变化规律,找出图形与数字之间的运算规律,利用规律解决问题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
柏拉图借毕达哥拉斯主义者提马尤斯门(Timaeus)的口说出以下的话:“两个东西不可能有完美的结合,除非另有第三者存在其间,因为他们之间必须有一种结合物,最好的结合物是比例.设有三个数量,若中数与小数之比等于大数与中数之比,反过来,小数与中数之比等于中数与大数之比--则后项就是前项和中数,中数就是前项和后项,所以三者必然相同,即为相同,就是一体”请问柏拉图在谈论的是什么数学概念,这个数学概念中涉及到的一个实数是什么?( )
| A、圆周率π | ||||
| B、勾股定理(毕达哥拉斯定理) 3:4:5 | ||||
C、黄金分割
| ||||
| D、黄金密度19.8千克/立方米 |
化简3a-2a的结果是( )
| A、1 | B、a | C、5a | D、5 |
已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=-|a1+1|,a3=-|a2+2|,a4=-|a3+3|,…依此类推,则a2014的值为( )
| A、-1005 | B、-1006 | C、-1007 | D、-2012 |
 如图,在半径为1的圆中,过圆上一定点A可以画3条长为整数的弦;在半径为2的圆中,过圆上一定点A可以画7条长为整数的弦;在半径为3的圆中,过圆上一定点A可以画11条长为整数的弦;那么,在半径为10的圆中,过圆上一定点A可以画长为整数的弦( )
如图,在半径为1的圆中,过圆上一定点A可以画3条长为整数的弦;在半径为2的圆中,过圆上一定点A可以画7条长为整数的弦;在半径为3的圆中,过圆上一定点A可以画11条长为整数的弦;那么,在半径为10的圆中,过圆上一定点A可以画长为整数的弦( )| A、21条 | B、35条 | C、39条 | D、43条 |
下列各式不是方程的是( )
| A、x2+x=0 | ||
| B、x+y=0 | ||
C、
| ||
| D、x=0 |
下列图形中,不是正方体表面展开图的是( )
A、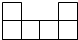 | B、 | C、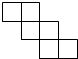 | D、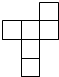 |




