Question

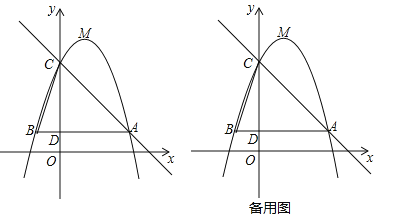
【题目】如图，已知一次函数y=mx+5的图象经过点A（1，4）、B（n ， 2）.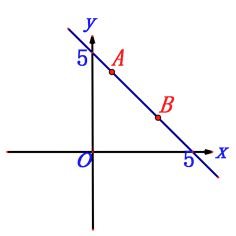

（1）求m、n的值；
（2）当函数图象在第一象限时，自变量x的取值范围是什么？
（3）在x轴上找一点P，使PA+PB最短。求出点P的坐标.

Answer 1

【答案】
（1）

解：将A（1，4）代入y= mx+5得：

4=m+5

解得：m= -1

∴y= -x+5

将B（n，2）代入y= -x+5得：

2= -n+5

解得：n=3

∴m、 n的值分别是-1、3

（2）

解：依题可得：

∴0＜x＜5

（3）

解：作点A关于x轴的对称点A′

∵A（1，4）

∴A′(1，-4)

连接A′B交x轴于点P，此时点P为所求的点

设直线A′B的解析式为y= kx+b，将A′(1，-4)、B（3，2）得：

解得：

∴直线A′B的解析式为：

当y=0时，

解得：

∴P（ ，0）

【解析】（1）将A（1，4）代入y= mx+5得m= -1，所以y= -x+5；再将B（n ， 2）代入y= -x+5得：n=3。
（2）由函数图像在第一象限可以得到一个二元一次方程组,解此方程即可。
（3）作点A（1，4）关于x轴的对称点A′(1，-4)，连接A′B交x轴于点P，此时点P为所求的点。用待定系数法的得到一个二元一次方程组:
.从而求得直线A′B的解析式为：y=3x7 ；令y=0即可求得P（ ，0）.
【考点精析】通过灵活运用确定一次函数的表达式和轴对称-最短路线问题，掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法；已知起点结点，求最短路径；与确定起点相反，已知终点结点，求最短路径；已知起点和终点，求两结点之间的最短路径；求图中所有最短路径即可以解答此题．