题目内容
已知:如图,点O是△ABC的边AC上一点,MN过O点且与BC平行,∠BCA的内、外角的角平分线交MN于D、E点,问:当O点在AC上移动时,四边形ADCE是否能成为矩形,证明你的结论。
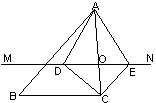
当点O在AC边的中点时,四边形ADCE能成为矩形。
证明:∵点O是AC边的中点,
∴AO=CO,
∵MN∥BC,
∴∠ODC=∠DCB,
∵CD平分∠ACB,
∴∠DCB=∠DCO,
∴∠ODC=∠DCO,
∴OD=OC,
同理 OE=OC,
∴OD=OE,
∴四边形ADCE是平行四边形,
∵AC=2OC,DE=2OD,OC=OD
∴AC=DE,
∴四边形ADCE是矩形。
证明:∵点O是AC边的中点,
∴AO=CO,
∵MN∥BC,
∴∠ODC=∠DCB,
∵CD平分∠ACB,
∴∠DCB=∠DCO,
∴∠ODC=∠DCO,
∴OD=OC,
同理 OE=OC,
∴OD=OE,
∴四边形ADCE是平行四边形,
∵AC=2OC,DE=2OD,OC=OD
∴AC=DE,
∴四边形ADCE是矩形。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 BA.
BA.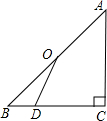 已知:如图,点O是等腰直角△ABC斜边AB的中点,D为BC边上任意一点.
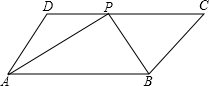
已知:如图,点O是等腰直角△ABC斜边AB的中点,D为BC边上任意一点. 10、已知:如图,点P是正方形ABCD的对角线AC上的一个动点(A、C除外),作PE⊥AB于点E,作PF⊥BC于点F,设正方形ABCD的边长为x,矩形PEBF的周长为y,在下列图象中,大致表示y与x之间的函数关系的是( )
10、已知:如图,点P是正方形ABCD的对角线AC上的一个动点(A、C除外),作PE⊥AB于点E,作PF⊥BC于点F,设正方形ABCD的边长为x,矩形PEBF的周长为y,在下列图象中,大致表示y与x之间的函数关系的是( )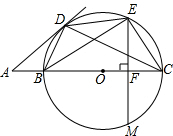 B=∠DEB,EF⊥BC于点F,交⊙O于点M,EM=2
B=∠DEB,EF⊥BC于点F,交⊙O于点M,EM=2 25、已知:如图,点D是△ABC的边AC上的一点,过点D作DE⊥AB,DF⊥BC,E、F为垂足,再过点D作DG∥AB,交BC于点G,且DE=DF.
25、已知:如图,点D是△ABC的边AC上的一点,过点D作DE⊥AB,DF⊥BC,E、F为垂足,再过点D作DG∥AB,交BC于点G,且DE=DF.