题目内容
已知:如图,点P是平行四边形ABCD的边DC上一点,且AP和BP分别平分∠DAB和∠C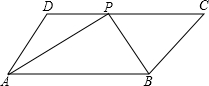 BA.
BA.(1)求证:AP⊥PB;
(2)如果AD=5,AP=8,求△APB的面积.
分析:(1)根据平行四边形的同旁内角互补,再结合角平分线的定义,可以得到∠PAB+∠PBA=90°,再根据三角形的内角和定理就可证明;
(2)根据角平分线的定义以及两条直线平行,则内错角相等.从而证明△ADP和△BCP是等腰三角形.则AB=CD=PD+PC=2AD=10,根据勾股定理得到PB=6,再根据直角三角形的面积等于两条直角边的乘积的一半.
(2)根据角平分线的定义以及两条直线平行,则内错角相等.从而证明△ADP和△BCP是等腰三角形.则AB=CD=PD+PC=2AD=10,根据勾股定理得到PB=6,再根据直角三角形的面积等于两条直角边的乘积的一半.
解答:(1)证明:∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB=
∠DAB,∠PBA=
∠CBA.
又∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠PAB+∠PBA=90°.
∴∠APB=180°-90°=90°.从而AP⊥PB.
(2)解:∵四边形ABCD是平行四边形,
∴BC=AD=5.
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB=∠PAD=∠DPA.
∴DP=AD=5.
同理PC=BC=5.
∴AB=DC=DP+PC=10.
∴在Rt△APB中,应用勾股定理得:BP=
=
=6.
∴△APB的面积是
AP•BP=
×8×6=24.
∴∠PAB=
| 1 |
| 2 |
| 1 |
| 2 |
又∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠PAB+∠PBA=90°.
∴∠APB=180°-90°=90°.从而AP⊥PB.
(2)解:∵四边形ABCD是平行四边形,
∴BC=AD=5.
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB=∠PAD=∠DPA.
∴DP=AD=5.
同理PC=BC=5.
∴AB=DC=DP+PC=10.
∴在Rt△APB中,应用勾股定理得:BP=
| AB2-AP2 |
| 102-82 |
∴△APB的面积是
| 1 |
| 2 |
| 1 |
| 2 |
点评:根据平行线的性质结合角平分线的定义,发现两个等腰三角形ADP和等腰三角形BCP,再根据直角三角形的勾股定理进行计算.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
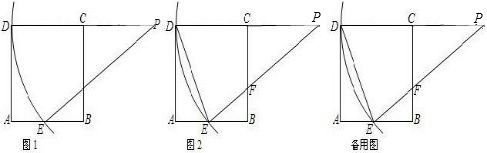
 时,△AB′B与△BEF是否相似?若相似,请加以证明;若不相似,简要说明理由.
时,△AB′B与△BEF是否相似?若相似,请加以证明;若不相似,简要说明理由.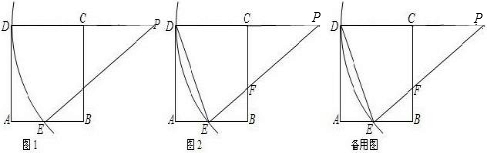
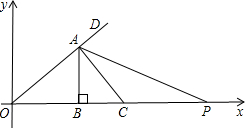
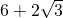 ,0)处有一小球正向坐标原点做匀速直线运动,已知小球滚动的速度与机器人行走的速度相同,若忽略机器人原地旋转的时间,请你给机器人发一个指令,使它能最快截住小球.(如图,点C为机器人最快截住小球的位置,要求写出计算过程)
,0)处有一小球正向坐标原点做匀速直线运动,已知小球滚动的速度与机器人行走的速度相同,若忽略机器人原地旋转的时间,请你给机器人发一个指令,使它能最快截住小球.(如图,点C为机器人最快截住小球的位置,要求写出计算过程)
 时,△AB′B与△BEF是否相似?若相似,请加以证明;若不相似,简要说明理由.
时,△AB′B与△BEF是否相似?若相似,请加以证明;若不相似,简要说明理由.