题目内容
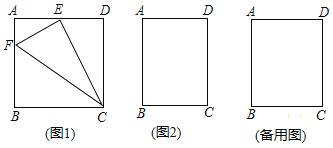
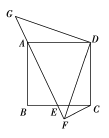
【题目】如图,正方形ABCD的顶点A在等腰直角三角形DFG的斜边FG上,G与BC相交于点E,连接CF.
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)若正方形ABCD的边长为2,点E是BC的中点,求FG的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)根据正方形和等腰直角三角形的边长相等可以得到两组对应边,再用直角去掉公共角得到一组对应角,即可判定全等.
(2)由(1)的全等推出∠CFE为直角,即可利用一组直角和一组对顶角判定![]() .
.
(3)根据![]() 得到对应边成比例,将线段代入求出CF,EF,再由
得到对应边成比例,将线段代入求出CF,EF,再由![]() 得到AG=CF,即可算出FG.
得到AG=CF,即可算出FG.
(1)∵四边形ABCD是正方形,![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
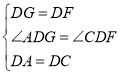 ,
,
∴![]() (SAS).
(SAS).
(2)由(1)知![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() .
.
(3)由(2)知![]() ,
,
∴![]() ,
,
∵正方形ABCD的边长为2,点E是BC的中点,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
由(1)知![]() ,
,![]() ,
,
∴![]() .
.

练习册系列答案
相关题目