题目内容
【题目】如图,已知E、F为平行四边形ABCD的对角线上的两点,且BE=DF,∠AEC=90°.求证:四边形AECF为矩形. 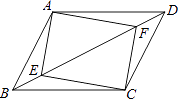
【答案】证明:连接AC交BD于O,如图所示: ∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵BE=DF,
OE=OF.
∵OA=OC,
∴AECF是平行四边形;
∵∠AEC=90°,
∴四边形AECF为矩形.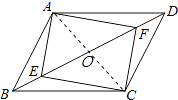
【解析】连接AC交BD于O,由平行四边形的性质得出OA=OC,OB=OD,由已知条件得出OE=OF,证出四边形AECF为平行四边形,再由∠AEC=90°,即可得出结论.
【考点精析】利用平行四边形的性质和矩形的判定方法对题目进行判断即可得到答案,需要熟知平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目