题目内容
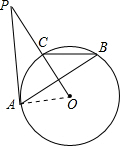
如图,PA与⊙O相切,切点为A,PO交⊙O于点C,点B是优弧CBA上一点,若∠ABC=32°,则∠P的度数为______.


连接OA.
∴∠PAO=90°,
∵∠O=2∠B=64°,
∴∠P=90°-64°=26°.
故答案为:26°.
∴∠PAO=90°,
∵∠O=2∠B=64°,
∴∠P=90°-64°=26°.
故答案为:26°.


练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
 CP一定是______三角形.
CP一定是______三角形.






