��Ŀ����
����Ŀ�������壩��ƽ��ֱ������ϵ�У����ں���ͼ��ĺ�����ݸ߸������¶��壺���Ա���x��![]() ��Χ��ʱ������ֵy����
��Χ��ʱ������ֵy����![]() ����ô���dz�b-aΪ��κ���ͼ��ĺ������d-cΪ��κ���ͼ����ݸߣ��ݸ������ı�ֵ��Ϊk����
����ô���dz�b-aΪ��κ���ͼ��ĺ������d-cΪ��κ���ͼ����ݸߣ��ݸ������ı�ֵ��Ϊk����![]() ��
��
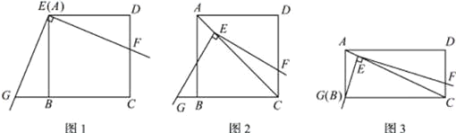
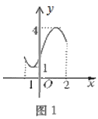
��ʾ������ͼ1����![]() ʱ������ֵy����
ʱ������ֵy����![]() ����ô�öκ���ͼ��ĺ��Ϊ2-��-1��=3���ݸ�Ϊ4-1=3����
����ô�öκ���ͼ��ĺ��Ϊ2-��-1��=3���ݸ�Ϊ4-1=3����![]() ��
��
��Ӧ�ã���1����![]() ʱ������
ʱ������![]() ��ͼ����Ϊ ���ݸ�Ϊ ��
��ͼ����Ϊ ���ݸ�Ϊ ��
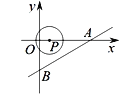
��2����֪����������![]() ������M(3��4)�͵�N�ڸú���ͼ���ϣ���MN�κ���ͼ����ݸ�Ϊ2ʱ����k��ֵ��
������M(3��4)�͵�N�ڸú���ͼ���ϣ���MN�κ���ͼ����ݸ�Ϊ2ʱ����k��ֵ��
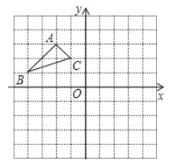
��3����֪���κ���![]() ��ͼ����x�ύ��A�㣬B�㣮
��ͼ����x�ύ��A�㣬B�㣮
����m=1���Ƿ���������������߶Σ���![]() (
(![]() )ʱ������ֵ����
)ʱ������ֵ����![]() �����ڣ��������κ���ͼ���kֵ���������ڣ���˵�����ɣ�
�����ڣ��������κ���ͼ���kֵ���������ڣ���˵�����ɣ�
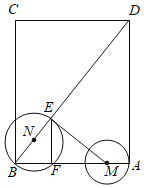
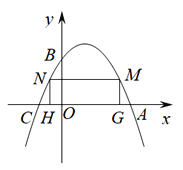
����ͼ2������P��ֱ��y=x���˶����Ե�PΪԲ�ģ�![]() Ϊ�뾶��Բ����AB�κ���ͼ���k=1ʱ�������߶���ǡ������
Ϊ�뾶��Բ����AB�κ���ͼ���k=1ʱ�������߶���ǡ������![]() �ϣ���ֱ��д����ʱ��P�����꣮
�ϣ���ֱ��д����ʱ��P�����꣮

���𰸡���1��2��4����2��![]() ��2����3���ٴ��ڣ�k=3����
��2����3���ٴ��ڣ�k=3���� ![]() ��
��![]() ��
��![]()
��������
��1����![]() ʱ������
ʱ������![]() �ĺ���ֵy����
�ĺ���ֵy����![]()
�Ӷ����Եó�������ݸߣ�
��2��������MN�κ���ͼ����ݸ�Ϊ2���������з�������N��yֵΪ2�Լ�6��������ٸ������ж�kֵ����Ĺ�ʽ���м��㼴�ɣ�
��3��������������Ľ���ʽ���Գ��ἰ���ֵ�����ݺ���ֵ����![]() ȷ��b��ȡֵ��Χ�����жϴ�ʱ�����������ԣ�ȷ�������˵�����꣬���뺯������ʽ��⼴�ɣ�
ȷ��b��ȡֵ��Χ�����жϴ�ʱ�����������ԣ�ȷ�������˵�����꣬���뺯������ʽ��⼴�ɣ�
�������A��B�����꼰�������꣬����k=1���m��ֵ��������������ۼ��ɣ�
��1����![]() ʱ������
ʱ������![]() �ĺ���ֵy����
�ĺ���ֵy����![]() ��
��
�Ӷ����Եó����Ϊ![]() ���ݸ�Ϊ
���ݸ�Ϊ![]()
�ʴ�Ϊ��2��4��
��2����M��3��4�����룬��n=12��
![]() �ݸ�Ϊ2��
�ݸ�Ϊ2��
![]() ��y=2����x=6����y=6��x=2��
��y=2����x=6����y=6��x=2��
![]() ��
��
![]() .
.
��3���ٴ��ڣ�
![]() ��
��
![]() ����ʽ�ɻ�Ϊ
����ʽ�ɻ�Ϊ![]() ��
��
![]() ��x=2ʱ��y���ֵΪ4��
��x=2ʱ��y���ֵΪ4��
![]() �����
�����![]() ��
��
![]() ��
��![]() ʱ��ͼ���ڶԳ�����࣬
ʱ��ͼ���ڶԳ�����࣬
![]() y��x�����������
y��x�����������
![]() ��x=aʱ��y=2a����x=bʱ��y=3b����
��x=aʱ��y=2a����x=bʱ��y=3b����![]() �ֱ���뺯������ʽ��
�ֱ���뺯������ʽ��
���![]() (��)��
(��)��![]() (��)��
(��)��![]() ��
��
![]()
��![]() ��
��![]() ��
��![]() �������ǣ�
�������ǣ�
![]()
![]() A��0��0����B��4��0��������K��2��4m����
A��0��0����B��4��0��������K��2��4m����
![]() AB�κ���ͼ���k=1��
AB�κ���ͼ���k=1��
![]() ��
��
![]() m=1��-1��
m=1��-1��
![]() ���κ���Ϊ
���κ���Ϊ![]() ��
��![]() ��������K��P��ֱ���x�ᡢy��Ĵ��ߣ�����ΪH.
��������K��P��ֱ���x�ᡢy��Ĵ��ߣ�����ΪH.
i)�����κ���Ϊ![]() ��
��
��ͼ1����P������Ϊ��x��x������KH=![]() ��PH=
��PH=![]() ��
��
��![]() ��
��![]() ��
��
��![]()
���![]() ��
��
![]()
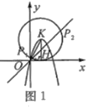
ii)�����κ���Ϊ![]() ��
��
��ͼ2����P������Ϊ��x��x������![]() ��
��
��![]() ��
�У�![]()
![]() �����x=-1��
�����x=-1��
![]()