Question

【题目】如图，∠MON=α（0＜α＜90°），A为OM上一点（不与O重合），点A关于直线ON的对称点为B，AB与ON交于点C，P为直线ON上一点（不与O，C重合）将射线PB绕点P顺时针旋转β角，其中2α+β=180°，所得到的射线与直线OM交于点Q．这个问题中，点的位置和角的大小都不确定，在这里我们仅研究两种特殊情况，一般的情况留给同学们深入探索．

（1）如图1，当α=45°时，此时β=90°，若点P在线段OC的延长线上．

①依题意补全图形；

②求∠PQA﹣∠PBA的值；

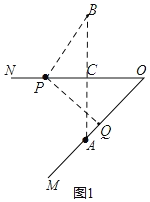
（2）如图2，当α=60°，点P在线段CO的延长线上时，用等式表示线段OC，OP，AQ之间的数量关系，并证明．

Answer 1

【答案】（1）①见解析；②45°；（2）AQ＝4OC+OP，理由见解析.

【解析】

（1）①依据题意可得图形；

②通过轴对称的性质，旋转的性质，可求AB⊥OP，BP⊥PQ，可得∠PBA=∠OPQ，即可求∠PQA﹣∠PBA的值；

（2）在OQ上截取OD=OP，连接BO，PD，BQ，由题意可得∠BON=∠MON=∠POQ=60°，∠BPQ=β=180°﹣2α=60°，可证点B，点Q，点P，点O四点共圆，可得∠PBQ=∠POQ=60°，∠PBO=∠OQP，由“AAS”可证△BOP≌△QDP，可得DQ=OB=OA=2OC，即可求线段OC，OP，AQ之间的数量关系．

（1）①

②∵点A，点B关于ON对称，∴AB⊥ON，∴∠PBA+∠BPC=90°．

∵∠BPQ=90°，∴∠BPC+∠OPQ=90°，∴∠OPQ=∠PBA．

∵∠PQA=∠O+∠OPQ，∴∠PQA=∠O+∠PBA，∴∠PQA﹣∠PBA=∠O=45°．

（2）AQ=4OC+OP．理由如下：

在OQ上截取OD=OP，连接BO，PD，BQ．

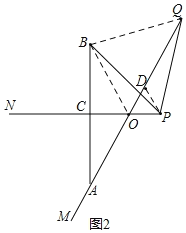
∵∠MON=α=60°，且点A关于直线ON的对称点为B，∴∠BON=∠MON=∠POQ=60°，AO=BO，CO⊥AB，∴∠BOQ=60°，∠CAO=30°，∴AO=2CO．

∵旋转，∴∠BPQ=β=180°﹣2α=60°，∴∠BOQ=∠BPQ=60°，∴点B，点Q，点P，点O四点共圆，∴∠PBQ=∠POQ=60°，∠PBO=∠OQP，∴△PBQ是等边三角形，∴PB=PQ．

∵OD=OP，∠QOP=60°，∴△ODP是等边三角形，∴∠ODP=∠DOP=60°，∴∠BOP=∠PDQ=120°，且BP=PQ，∠OBP=∠OQP，∴△BOP≌△QDP（AAS），∴DQ=OB，∴DQ=OA=2OC，∴AQ=AO+OQ=2CO+OD+PQ=4OC+OP．