题目内容
【题目】如图,在平面直角坐标系中,点![]() ,点
,点![]() ,点
,点![]() 是直线
是直线![]() 上一点,且
上一点,且![]() ,则点
,则点![]() 的坐标为____.
的坐标为____.

【答案】(3,-4)
【解析】
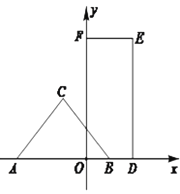
将△BOA绕点B顺时针旋转90°得到△BED,可求出D点坐标,DE交x轴于F,连接AD,取AD中点C,连接BC并延长交直线y=-x-1于P,可求出C点坐标,进而可得 直线BC的解析式,由等腰直角三角形的性质可得∠ABC=45°,可得直线BC与直线y=-x-1的交点即为点P,利用方程组求出点P坐标即可.
将线△BOA绕点B顺时针旋转90°得到△BED,DE交x轴于F,连接AD,取AD中点C,连接BC并延长交直线y=-x-1于P,
∵A(6,0),B(0,2),
∴OB=2,OA=6,
∴BE=OB=2,ED=OA=6,AB=BD,∠BED=∠BOA=90°,∠OBE=90°,∠ABD=90°,
∴四边形EFOB是矩形,
∴EF=OB=2,
∴DF=DE-EF=4,
∴D(-2,-4),
∵AB=BD,C为AD中点,∠ABD=90°,
∴∠ABC=45°,
∴直线BC与直线y=-x-1的交点即为点P,
∵A(6,0),D(-2,-4)
∴C(2,-2),
设直线BC的解析式为y=kx+b,
∴![]() ,
,
解得:![]() ,
,
∴直线BC的解析式为y=-2x+2,
联立直线BC与直线y=-x-1得:![]() ,
,
解得:![]() ,
,
∴点P坐标为(3,-4).

故答案为:(3,-4)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目