题目内容
【题目】在如图所示的平面直角坐标系中，直线AB：y=k1x+b1与直线AD：y=k2x+b2相交于点A（1，3），且点B坐标为（0，2），直线AB交x轴负半轴于点C，直线AD交x轴正半轴于点D．
（1）求直线AB的函数解析式；
（2）若△ACD的面积为9，解不等式：k2x+b2＞0；
（3）若点M为x轴一动点，当点M在什么位置时，使AM+BM的值最小？求出此时点M的坐标．
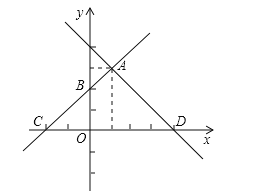
【答案】（1）y=x+2；（2）x＜4；（3）（
，0）．
【解析】
（1）将点A、B两点代入，即可求解析式；
（2）令y=0，求出C点坐标，由三角形ACD的面积是9，求出D点坐标，结合图象即可求解；
（3）作点B关于x轴的对称点E（0，-2），连接AE交x轴于点M，设直线AE解析式为y=kx+b，确定AE的解析式即可求M点坐标．
解：（1）把A、B两点代入，得
，
解得
，
故直线AB的函数解析式为y=x+2；
（2）令y=x+2=0得x=-2，
∴C（-2，0）.
又∵△ACD的面积为9，
∴
3×CD=9，
∴CD=6，
∴D点坐标（4，0），
由图象得不等式的解集为：x＜4；
（3）作点B关于x轴的对称点E（0，-2），连接AE交x轴于点M，
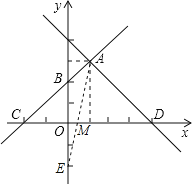
设直线AE解析式为y=kx+b，
∴
，
∴
，
∴y=5x-2，
当y=0时，x=，故点M的坐标为（，0）．
练习册系列答案
相关题目
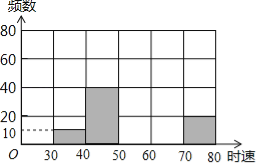
【题目】将某雷达测速区监测到的一组汽车的时速数据整理，得到其频数分布表（未完成）：
数据段 | 30～40 | 40～50 | 50～60 | 60～70 | 70～80 | 总计 |
频 数 | 10 | 40 | | | 20 | |
百分比 | 5% | | 40% | | 10% | |
注：30～40为时速大于等于30千米而小于40千米，其他类同．
（1）请你把表中的数据填写完整；
（2）补全频数分布直方图；
（3）如果此路段汽车时速超过60千米即为违章，则违章车辆共有多少辆？
