Question

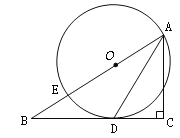
【题目】如图，在△ABC中，∠C=90°，点E在AB上，以AE为直径的⊙O与BC相切于点D，连接AD．

（1）求证：AD平分∠BAC；

（2）若⊙O的直径为10，sin∠DAC=，求BD的长.

Answer 1

【答案】（1）证明见解析；（2）

【解析】（1）连接OD，先根据平行线的判定定理证明OD∥AC，然后依据平行线的性质和等腰三角形的性质证明∠OAD=∠DAC，于是可证明AD平分∠BAC；

（2）连接ED、OD，由题意可知AE=10，接下来，在△ADA中，依据锐角三角形的定义可求得AD的长，然后在△ADC中，可求得DC和AC的长，由OD∥AC可证明△BOD∽△BAC，然后由相似三角形的性质可列出关于BD的方程.

解：（1）如图1，连接OD．

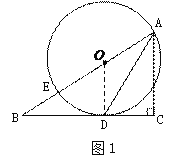
∵⊙O与BC相切于点D，

∴OD⊥BC，

∴∠ODB=90°，

∵∠C=90°，

∴∠C=∠ODB，

∴OD∥AC，

∴∠ODA=∠DAC，

∵OD=OA，

∴∠OAD=∠ODA，

∴∠OAD=∠DAC，

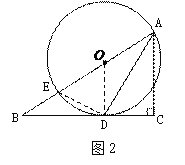
∴AD平分∠BAC．

（2）如图2，连接ED．

∵⊙O的直径为10，AE是⊙O的直径，

∴AE=10，∠EDA=90°，

∵∠EAD=∠DAC，sin∠DAC=，

∴sin∠EAD==，

∴DE=，

∴AD==，

同理可求DC=4，AC=8，

∵OD∥AC，

∴△BOD∽△BAC，

∴=，即=，解得：BD=．

“点睛”本题主要考查的是切线的性质、平行线的判定和性质、等腰三角形的性质、锐角三角函数的定义、相似三角形的判定和性质，列出关于BD的方程是解题的关键.