题目内容
已知:如图,在矩形ABCD中,点E在AD边上,AE>DE,BE=BC,点O是线段CE的中点.
(1)试说明CE平分∠BED;
(2)若AB=3,BC=5,求BO的长;
(3)在直线AD上是否存在点F,使得以B、C、F、E为顶点的四边形是菱形?如果存在,试画出点F的位置,并作适当说明;如果不存在,请说明理由.
分析:(1)根据矩形的性质AD∥BC,所以∠BCE=∠DEC,再根据等腰三角形三线合一的性质求解即可;
(2)利用勾股定理先求出AE、EC的长,在△BCO中根据勾股定理即可求出BO;
(3)因为邻边BE、BC相等,所以只要作出的是平行四边形就可以,在ED延长线上可以,而在EA的延长线上不能作出以BC、BE为邻边的平行四边形.
(2)利用勾股定理先求出AE、EC的长,在△BCO中根据勾股定理即可求出BO;
(3)因为邻边BE、BC相等,所以只要作出的是平行四边形就可以,在ED延长线上可以,而在EA的延长线上不能作出以BC、BE为邻边的平行四边形.
解答:解:(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠BCE=∠DEC,(1分)
又∵BE=BC,∴∠BCE=∠BEC.(2分)
∴∠BEC=∠DEC,
∴CE平分∠BED.(3分)
(2)在Rt△BAE中,AB=3,BE=BC=5,
∴AE=4,(4分)
在Rt△CDE中,CD=3,DE=1,
∴EC=
,(5分)
在Rt△BOC中,BC=5,CO=
,
∴BO=
=
=
,(6分)
(注:此处用等面积法求BO亦可,此处写
,不扣分)
(3)在直线AD上存在点F,使得以B、C、F、E为顶点的四边形是菱形.
延长ED至F,使得EF=BC,此时四边形BCFE是菱形.(7分)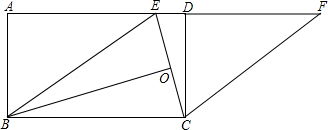
∵AE>DE,∴BE>CE,
因此在EA的延长线上不存在点F,使得四边形BCEF为菱形.(8分)
∴AD∥BC,
∴∠BCE=∠DEC,(1分)
又∵BE=BC,∴∠BCE=∠BEC.(2分)
∴∠BEC=∠DEC,
∴CE平分∠BED.(3分)
(2)在Rt△BAE中,AB=3,BE=BC=5,
∴AE=4,(4分)
在Rt△CDE中,CD=3,DE=1,
∴EC=
| 10 |
在Rt△BOC中,BC=5,CO=
| ||
| 2 |
∴BO=
| BC2-CO2 |
52-(
|
3
| ||
| 2 |
(注:此处用等面积法求BO亦可,此处写
| ||
| 2 |
(3)在直线AD上存在点F,使得以B、C、F、E为顶点的四边形是菱形.
延长ED至F,使得EF=BC,此时四边形BCFE是菱形.(7分)

∵AE>DE,∴BE>CE,
因此在EA的延长线上不存在点F,使得四边形BCEF为菱形.(8分)
点评:本题主要利用矩形的性质、等腰三角形的性质和勾股定理,熟练掌握并灵活运用是解题的关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 已知,如图,在矩形ABCD中,P是边AD上的动点,PE垂直AC于E,PF垂直BD于F,如果AB=3,AD=4,那么( )
已知,如图,在矩形ABCD中,P是边AD上的动点,PE垂直AC于E,PF垂直BD于F,如果AB=3,AD=4,那么( )A、PE+PF=
| ||||
B、
| ||||
| C、PE+PF=5 | ||||
| D、3<PE+PF<4 |
 已知,如图,在矩形ABCD中,M是边BC的中点,AB=3,BC=4,⊙D与直线AM相切于点E,
已知,如图,在矩形ABCD中,M是边BC的中点,AB=3,BC=4,⊙D与直线AM相切于点E, 已知:如图,在矩形ABCD中,AC是对角线.点P为矩形外一点且满足AP=PC,AP⊥PC.PC交AD于点N,连接DP,过点P作PM⊥PD交AD于M.
已知:如图,在矩形ABCD中,AC是对角线.点P为矩形外一点且满足AP=PC,AP⊥PC.PC交AD于点N,连接DP,过点P作PM⊥PD交AD于M. 已知:如图,在矩形ABCD中,AB=4,AD=10,F是AD上一点,CF⊥EF于点F交AB于点E,
已知:如图,在矩形ABCD中,AB=4,AD=10,F是AD上一点,CF⊥EF于点F交AB于点E, 已知:如图,在矩形ABCD中,对角线AC与BD相交于点O,BE⊥AC于E,CF⊥BD于F,请你判断BE与CF的大小关系,并说明你的理由.
已知:如图,在矩形ABCD中,对角线AC与BD相交于点O,BE⊥AC于E,CF⊥BD于F,请你判断BE与CF的大小关系,并说明你的理由.