��Ŀ����
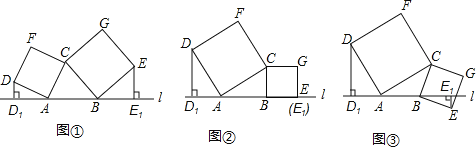
����Ŀ����ͼ����ʾ����֪A��BΪֱ��l�����㣬��CΪֱ��l�Ϸ�һ���㣬����AC��BC���ֱ���AC��BCΪ�����ABC����������CADF��������CBEG������D��DD1��l�ڵ�D1������E��EE1��l�ڵ�E1��
��1����ͼ�ڣ�����Eǡ����ֱ��l��ʱ����ʱE1��E�غϣ�����˵��DD1=AB��
��2����ͼ���У���D��E���㶼��ֱ��l���Ϸ�ʱ����̽�������߶�DD1��EE1��AB֮���������ϵ����˵�����ɣ�
��3����ͼ�ۣ�����E��ֱ��l���·�ʱ����ֱ��д�������߶�DD1��EE1��AB֮���������ϵ��������Ҫ֤����
���𰸡���1��֤�������������2��AB=DD1+EE1����3��AB=DD1-EE1��
�������������������1�����ı���CADF��CBEG�������οɵ�AD=CA����DAC=��ABC=90��������ͬ�ǵ������ȣ������ADD1=��CAB��Ȼ������AAS֤����ADD1�ա�CAB������ȫ�������εĶ�Ӧ����ȣ����ɵ�DD1=AB��
��2�����ȹ���C��CH��AB��H����DD1��AB���ɵ���DD1A=��CHA=90�������ı���CADF�������Σ��ɵ�AD=CA������ͬ�ǵ������ȣ������ADD1=��CAH��Ȼ������AAS֤����ADD1�ա�CAH������ȫ�������εĶ�Ӧ����ȣ����ɵ�DD1=AH��ͬ��EE1=BH����ɵ�AB=DD1+EE1��
��3��֤������ͬ��2�������ɵõ�AB=DD1-EE1��
�����������1����Ϊ�ı���CADF��CBEG�������Σ�
����AD=CA����DAC=��ABC=90����
������DAD1+��CAB=90����
��ΪDD1��AB��
������DD1A=��ABC=90����
������DAD1+��ADD1=90����
������ADD1=��CAB��
����ADD1����CAB��
��ADD1=��CAB����DD1A=��ABC ��AD=CA��
������ADD1�ա�CAB��
����DD1=AB��
��2��AB=DD1+EE1���������£�
����C��CH��AB��H ���루1��ͬ������ADD1�ա�CAH������DD1=AH��ͬ��EE1=BH������AB=DD1+EE1��
��3��AB=DD1-EE1���������£�
����C��CH��AB��H ���루1��ͬ������ADD1�ա�CAH������DD1=AH��ͬ��EE1=BH������AB=DD1-EE1��


