题目内容
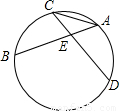
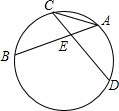 如图,弧BC与弧AD的度数相等,弦AB与弦CD交于点E,∠CEB=80°,则∠CAB等于
如图,弧BC与弧AD的度数相等,弦AB与弦CD交于点E,∠CEB=80°,则∠CAB等于
- A.30°
- B.40°
- C.45°
- D.60°
B
分析:根据等弧所对的圆周角相等,得∠A=∠C.再根据三角形的外角的性质,得∠A=∠C=80°÷2=40°.
解答:∵弧BC=弧AD
∴∠A=∠C
∵∠CEB=∠A+∠C=2∠A
∴∠A= ∠CEB=40°.
∠CEB=40°.
故选B.
点评:熟练掌握圆周角定理的推论,结合三角形外角的性质进行求解.
分析:根据等弧所对的圆周角相等,得∠A=∠C.再根据三角形的外角的性质,得∠A=∠C=80°÷2=40°.
解答:∵弧BC=弧AD
∴∠A=∠C
∵∠CEB=∠A+∠C=2∠A
∴∠A=
 ∠CEB=40°.
∠CEB=40°.故选B.
点评:熟练掌握圆周角定理的推论,结合三角形外角的性质进行求解.

练习册系列答案
相关题目
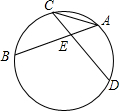 如图,弧BC与弧AD的度数相等,弦AB与弦CD交于点E,∠CEB=80°,则∠CAB等于( )
如图,弧BC与弧AD的度数相等,弦AB与弦CD交于点E,∠CEB=80°,则∠CAB等于( )| A、30° | B、40° | C、45° | D、60° |
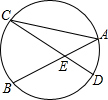 已知,如图,弧BC与AD的度数之差为20°,弦AB与CD交于点E,∠CEB=60°,则∠CAB=
已知,如图,弧BC与AD的度数之差为20°,弦AB与CD交于点E,∠CEB=60°,则∠CAB=