题目内容
【题目】在平面直角坐标系中,![]() 与
与![]() 轴交于点
轴交于点![]() ,将点
,将点![]() 向右平移两个单位长度,得到点
向右平移两个单位长度,得到点![]() ,点
,点![]() 在抛物线上.
在抛物线上.
(1)①直接写出抛物线的对称轴是__________;
②用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)横、纵坐标都是整数的点叫做整点.点![]() 恰好为整点,若抛物线在点
恰好为整点,若抛物线在点![]() 、
、![]() 之间的部分与线段
之间的部分与线段![]() 所围成的区域内(不含边界)恰有两个整点,结合函数图象,求
所围成的区域内(不含边界)恰有两个整点,结合函数图象,求![]() 的取值范围.
的取值范围.
【答案】(1)①直线x=-1;②b=-2a;(2)a的取值范围是![]() 或
或![]() .
.
【解析】
(1)①先求出点A的坐标得到点B的坐标,根据对称性即可得到对称轴;
②根据对称轴的公式计算即可得到;
(2)分两种情况:a>0或a<0,画出图形列不等式组求解.
(1)①当x=0时,得到y=-c,
∴点A的坐标为(0,-c),
∵将点![]() 向右平移两个单位长度,得到点
向右平移两个单位长度,得到点![]() ,
,
∴B(-2,-c),
∵点![]() 在抛物线上,
在抛物线上,
∴抛物线的对称轴是直线x=![]() =-1,
=-1,
故答案为:直线x=-1;
②∵对称轴是x=![]() =-1,
=-1,
∴b=-2a;
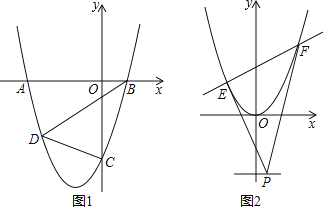
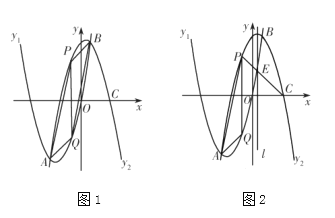
(2)如图,当a>0时,
∵A(0,-c),B(-2,-c),且指定区域内有两个整点,因此整点坐标必为(-1,-c-1)及(-1,-c-2),
∵抛物线的顶点坐标为(-1,-c-a),
∴![]() ,
,
解得![]() ;
;
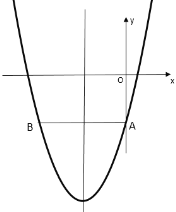
当a<0时,整点坐标必为(-1,-c+1)及(-1,-c+2)此两点必在区域内,
同理可得![]() ,
,
解得![]() ,
,
综上,a的取值范围是![]() 或
或![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】有一个圆形转盘,分黑色、白色两个区域.
(1)某人转动转盘,对指针落在黑色区域或白色区域进行了大量试验,得到数据如下表:
实验次数 | 10 | 100 | 2000 | 5000 | 10000 | 50000 | 100000 |
白色区域次数 | 3 | 34 | 680 | 1600 | 3405 | 16500 | 33000 |
落在白色区域频率 | 0.3 | 0.34 | 0.34 | 0.32 | 0.34 | 0.33 | 0.33 |
请你利用上述实验,估计转动该转盘指针落在白色区域的概率为___________.(精确到0.01);
(2)若该圆形转盘白色扇形的圆心角为120度,黑色扇形的圆心角为![]() ,转动转盘两次,求指针一次落在白色区域,另一次落在黑色区域的概率.
,转动转盘两次,求指针一次落在白色区域,另一次落在黑色区域的概率.