Question

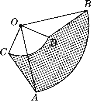
【题目】如图，扇形OAB与扇形OCD的圆心角都是90°，连接AC，BD.

(1)求证：AC＝BD；

(2)若OA＝2 cm，OC＝1 cm，求图中阴影部分的面积．

Answer 1

【答案】(1)证明见解析；(2) S阴影＝π(cm2)．

【解析】

（1）根据已知条件易证△AOC≌△BOD，由全等三角形的性质即可证得AC＝BD；（2）根据阴影部分的面积＝扇形OAB的面积－扇形OCD的面积即可求解．

(1)证明：∵∠AOB＝∠COD＝90°，

即∠AOC＋∠AOD＝∠BOD＋∠AOD，

∴∠AOC＝∠BOD.

又∵AO＝BO，CO＝DO，

∴△AOC≌△BOD，

∴AC＝BD.

(2)解：由(1)知△AOC≌△BOD，

∴阴影部分的面积＝扇形OAB的面积－扇形OCD的面积．

则S阴影＝－＝＝＝π(cm2)．