题目内容
在平面内,先将一个多边形以点O为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为k,并且原多边形上的任一点P,它的对应点P’ 在线段OP或其延长线上;接着将所得多边形以点O为旋转中心,逆时针旋转一个角度θ,这种经过放缩和旋转的图形变换叫做旋转相似变换,记为O( k, θ ),其中点O叫做旋转相似中心,k叫做相似比,θ叫做旋转角.
(1)填空:
①如图1,将△ABC以点A为旋转相似中心,放大为原来的2倍,再逆时针旋转60°,得到△ADE,这个旋转相似变换记为A( , );
②如图2,△ABC是边长为![]() 的等边三角形,将它作旋转相似变换A(
的等边三角形,将它作旋转相似变换A(![]() ,90°),得到△ADE,则线段BD的长为 cm;
,90°),得到△ADE,则线段BD的长为 cm;
(2)如图3,分别以锐角三角形ABC的三边AB、BC、CA为边向外作正方形ADEB、BFGC、CHIA,点O1、O2、O3分别是这三个正方形的对角线交点,试分别利用△AO1O3与△ABI、△CIB与△CAO2之间的关系,运用旋转相似变换的知识说明线段O1O3与AO2之间的关系.
 |
解:(1)①(![]() ,
,![]() );-----------2分
);-----------2分
②![]() ;--------------------4分
;--------------------4分
(2)△AO1O3经过旋转相似变换![]() ,得到
,得到![]() ,此时,线段O1O3变为线段
,此时,线段O1O3变为线段![]() ;------------------------------6分
;------------------------------6分
![]() 经过旋转相似变换
经过旋转相似变换 ,得到
,得到![]() ,此时,线段
,此时,线段![]() 变为线段AO2.------------------------------8分
变为线段AO2.------------------------------8分
![]() ,
,![]() ,
,
∴O1O3= AO2,O1O3⊥ AO2------10分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


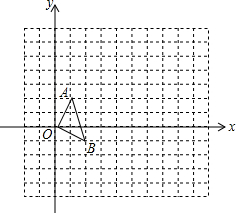 【问题】在正方形网格中,如图(一),△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).
【问题】在正方形网格中,如图(一),△OAB的顶点分别为O(0,0),A(1,2),B(2,-1). 为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为
为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为 ,并且原多边形上的任一点
,并且原多边形上的任一点 ,它的对应点
,它的对应点 在线段
在线段 或其延长线上;接着将所得多边形以点
或其延长线上;接着将所得多边形以点 ,这种经过和旋转的图形变换叫做旋转相似变换,记为
,这种经过和旋转的图形变换叫做旋转相似变换,记为 ,其中点
,其中点 以点
以点 为旋转相似中心,放大为原来的2倍,再逆时针旋转
为旋转相似中心,放大为原来的2倍,再逆时针旋转 ,得到
,得到 ,这个旋转相似变换记为
,这个旋转相似变换记为 的等边三角形,将它作旋转相似变换
的等边三角形,将它作旋转相似变换 ,得到
,得到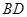 的长为
的长为  ;
; 的三边
的三边 ,
, ,
, 为边向外作正方形
为边向外作正方形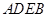 ,
, ,
, ,点
,点 ,
,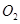 ,
, 分别是这三个正方形的对角线交点,试分别利用
分别是这三个正方形的对角线交点,试分别利用 与
与 ,
, 与
与 之间的关系,运用旋转相似变换的知识说明线段
之间的关系,运用旋转相似变换的知识说明线段 与
与 之间的关系.
之间的关系.
 为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为
为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为 ,并且原多边形上的任一点
,并且原多边形上的任一点 ,它的对应点
,它的对应点 在线段
在线段 或其延长线上;接着将所得多边形以点
或其延长线上;接着将所得多边形以点 ,这种经过和旋转的图形变换叫做旋转相似变换,记为
,这种经过和旋转的图形变换叫做旋转相似变换,记为 ,其中点
,其中点 以点
以点 为旋转相似中心,放大为原来的2倍,再逆时针旋转
为旋转相似中心,放大为原来的2倍,再逆时针旋转 ,得到
,得到 ,这个旋转相似变换记为
,这个旋转相似变换记为 的等边三角形,将它作旋转相似变换
的等边三角形,将它作旋转相似变换 ,得到
,得到 的长为
的长为  ;
; 的三边
的三边 ,
, ,
, 为边向外作正方形
为边向外作正方形 ,
, ,
, ,点
,点 ,
, ,
, 分别是这三个正方形的对角线交点,试分别利用
分别是这三个正方形的对角线交点,试分别利用 与
与 ,
, 与
与 之间的关系,运用旋转相似变换的知识说明线段
之间的关系,运用旋转相似变换的知识说明线段 与
与 之间的关系.
之间的关系.