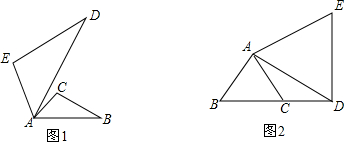题目内容
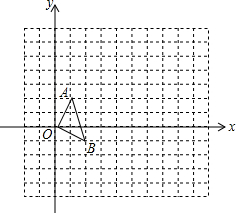 【问题】在正方形网格中,如图(一),△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).
【问题】在正方形网格中,如图(一),△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).(1)以点O(0,0)为位似中心,按比例尺3:1在位似中心的同侧将△OAB放大为△OA′B′,放大后点A、B的对应点分别为A′、B′.画出△OA′B′,并写出点A'、B'的坐标:A′(
3
3
,6
6
),B′(6
6
,-3
-3
);(2)在(1)中,若点C(a,b)为线段AB上任一点,写出变化后点C的对应点C′的坐标(
3a
3a
,3b
3b
);【拓展】在平面内,先将一个多边形以点O为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为k,并且原多边形上的任一点P,它的对应点P'在线段OP或其延长线上;接着将所得多边形以点O为旋转中心,逆时针旋转一个角度θ,这种经过和旋转的图形变换叫做旋转相似变换,记为O(k,θ),其中点O叫做旋转相似中心,k叫做相似比,θ叫做旋转角.
【探索】如图(二),完成下列问题:
(3)填空:如图1,将△ABC以点A为旋转相似中心,放大为原来的2倍,再逆时针旋转60°,得到△ADE,这个旋转相似变换记为A(
2
2
,60°
60°
);(4)如图2,△ABC是边长为3cm的等边三角形,将它作旋转相似变换A(
| 4 | 3 |

分析:(1)利用已知画出位似图形,进而得出A′,B′的坐标即可;
(2)利用(1)中点的坐标变化规律得出即可;
(3)依题意已知1中△ABC以点A为旋转相似中心,放大为原来的2倍,再逆时针旋转60°,得到△ADE,故可得A的坐标.
(4)利用△ABC旋转相似变换A(
,90°),得到△ADE,可推出∠BAD=90°,利用勾股定理可求出BD的值.
(2)利用(1)中点的坐标变化规律得出即可;
(3)依题意已知1中△ABC以点A为旋转相似中心,放大为原来的2倍,再逆时针旋转60°,得到△ADE,故可得A的坐标.
(4)利用△ABC旋转相似变换A(
| 4 |
| 3 |
解答: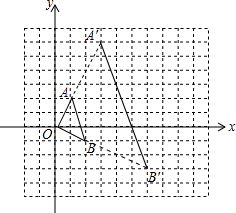 解:(1)∵以点O(0,0)为位似中心,按比例尺3:1在位似中心的同侧将△OAB放大为△OA′B′,
解:(1)∵以点O(0,0)为位似中心,按比例尺3:1在位似中心的同侧将△OAB放大为△OA′B′,
∴如图所示:A′(3,6),B′(6,-3);
故答案为:3,6;6,-3;
(2)根据(1)中规律可以得出:若点C(a,b)为线段AB上任一点,
故变化后点C的对应点C′的坐标为:(3a,3b);
故答案为:3a,3b;
(3)这种经过和旋转的图形变换叫做旋转相似变换,记为O(k,θ),其中点O叫做旋转相似中心,k叫做相似比,θ叫做旋转角.已知1中△ABC以点A为旋转相似中心,放大为原来的2倍,再逆时针旋转60°,得到△ADE,
故可得A(2,60°).
故答案为:(2,60°);
(4)已知△ABC旋转相似变换A(
,90°),得到△ADE以及AD=
×3=4(cm),
可推出∠BAD=90°,
利用勾股定理可求出BD=
=5(cm).
 解:(1)∵以点O(0,0)为位似中心,按比例尺3:1在位似中心的同侧将△OAB放大为△OA′B′,
解:(1)∵以点O(0,0)为位似中心,按比例尺3:1在位似中心的同侧将△OAB放大为△OA′B′,∴如图所示:A′(3,6),B′(6,-3);
故答案为:3,6;6,-3;
(2)根据(1)中规律可以得出:若点C(a,b)为线段AB上任一点,
故变化后点C的对应点C′的坐标为:(3a,3b);
故答案为:3a,3b;
(3)这种经过和旋转的图形变换叫做旋转相似变换,记为O(k,θ),其中点O叫做旋转相似中心,k叫做相似比,θ叫做旋转角.已知1中△ABC以点A为旋转相似中心,放大为原来的2倍,再逆时针旋转60°,得到△ADE,
故可得A(2,60°).
故答案为:(2,60°);
(4)已知△ABC旋转相似变换A(
| 4 |
| 3 |
| 4 |
| 3 |
可推出∠BAD=90°,
利用勾股定理可求出BD=
| 32+42 |
点评:此题主要考查了位似变换以及旋转的性质以及勾股定理等知识,利用相似变换的性质得出对应点的坐标是解题关键.

练习册系列答案
相关题目
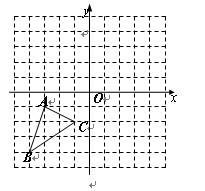
 为圆心,
为圆心, 为半径作圆
为半径作圆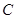 (如图(1)),过点
(如图(1)),过点 ,以点
,以点 为半径作圆交网格线于点
为半径作圆交网格线于点 (如图(2)).
(如图(2)).
 的度数;
的度数; ;
; 可以看作是由
可以看作是由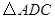 经过怎样的变换得到的?并判断
经过怎样的变换得到的?并判断 的形状(不用说明理由).
的形状(不用说明理由). ,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形
,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形 ,使三个顶点
,使三个顶点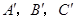 ,分别在直线
,分别在直线

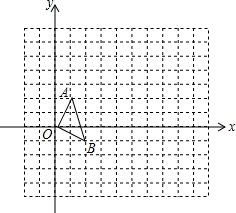 【问题】在正方形网格中,如图(一),△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).
【问题】在正方形网格中,如图(一),△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).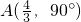 ,得到△ADE,求线段BD的长.
,得到△ADE,求线段BD的长.