题目内容
在平面内,先将一个多边形以点O为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为k,并且原多边形上的任一点P,它的对应点P′在线段OP或其延长线上;接着将所得多边形以点0为旋转中心,逆时针旋转一个角度θ,这种经过相似和旋转的图形变换叫做旋转相似变换,记为O(k,θ),其中点0叫做旋转相似中心,k叫做相似比,θ叫做旋转角.
(1)如图1,将△ABC以点A为旋转相似中心,放大为原来的2倍,再逆时针旋转60°,得到△ADE,这个旋转相似变换记为A(
(2)如图2,△ABC是边长为1cm的等边三角形,将它作旋转相似变换A(
,90°)得到△ADE,求线段BD的长.

(1)如图1,将△ABC以点A为旋转相似中心,放大为原来的2倍,再逆时针旋转60°,得到△ADE,这个旋转相似变换记为A(
2
2
,60°
60°
);(2)如图2,△ABC是边长为1cm的等边三角形,将它作旋转相似变换A(
| 3 |

分析:(1)依题意已知,△ABC以点A为旋转相似中心,放大为原来的2倍,再逆时针旋转60°,得到△ADE,故可得A的坐标.
(2)已知2中△ABC旋转相似变换A(
,90°),得到△ADE,可推出∠BAD=90°,利用勾股定理可求出BD的值.
(2)已知2中△ABC旋转相似变换A(
| 3 |
解答:解:(1)∵△ABC以点A为旋转相似中心,放大为原来的2倍,再逆时针旋转60°,得到△ADE,故可得A(2,60°),
∴在这个旋转相似变换过程中,旋转相似中心是A,相似比是2,旋转角是60°,
∴这个旋转相似变换记为A( 2,60°).
故答案是:2,60°;
(2)△ABC旋转相似变换A(
,90°),得到△ADE以及AD=
,可推出∠BAD=90°,
利用勾股定理得到:BD=
=2.
∴在这个旋转相似变换过程中,旋转相似中心是A,相似比是2,旋转角是60°,
∴这个旋转相似变换记为A( 2,60°).
故答案是:2,60°;
(2)△ABC旋转相似变换A(
| 3 |
| 3 |
利用勾股定理得到:BD=
(
|
点评:本题主要考查了几何变换综合题.解答该题的关键是弄清楚O(k,θ)所表达的含义,其中点0叫做旋转相似中心,k叫做相似比,θ叫做旋转角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

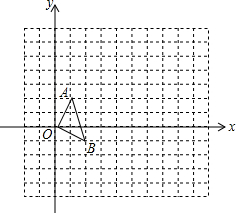 【问题】在正方形网格中,如图(一),△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).
【问题】在正方形网格中,如图(一),△OAB的顶点分别为O(0,0),A(1,2),B(2,-1). 为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为
为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为 ,并且原多边形上的任一点
,并且原多边形上的任一点 ,它的对应点
,它的对应点 在线段
在线段 或其延长线上;接着将所得多边形以点
或其延长线上;接着将所得多边形以点 ,这种经过和旋转的图形变换叫做旋转相似变换,记为
,这种经过和旋转的图形变换叫做旋转相似变换,记为 ,其中点
,其中点 以点
以点 为旋转相似中心,放大为原来的2倍,再逆时针旋转
为旋转相似中心,放大为原来的2倍,再逆时针旋转 ,得到
,得到 ,这个旋转相似变换记为
,这个旋转相似变换记为 的等边三角形,将它作旋转相似变换
的等边三角形,将它作旋转相似变换 ,得到
,得到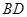 的长为
的长为  ;
; 的三边
的三边 ,
, ,
, 为边向外作正方形
为边向外作正方形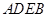 ,
, ,
, ,点
,点 ,
,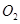 ,
, 分别是这三个正方形的对角线交点,试分别利用
分别是这三个正方形的对角线交点,试分别利用 与
与 ,
, 与
与 之间的关系,运用旋转相似变换的知识说明线段
之间的关系,运用旋转相似变换的知识说明线段 与
与 之间的关系.
之间的关系.
 为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为
为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为 ,并且原多边形上的任一点
,并且原多边形上的任一点 ,它的对应点
,它的对应点 在线段
在线段 或其延长线上;接着将所得多边形以点
或其延长线上;接着将所得多边形以点 ,这种经过和旋转的图形变换叫做旋转相似变换,记为
,这种经过和旋转的图形变换叫做旋转相似变换,记为 ,其中点
,其中点 以点
以点 为旋转相似中心,放大为原来的2倍,再逆时针旋转
为旋转相似中心,放大为原来的2倍,再逆时针旋转 ,得到
,得到 ,这个旋转相似变换记为
,这个旋转相似变换记为 的等边三角形,将它作旋转相似变换
的等边三角形,将它作旋转相似变换 ,得到
,得到 的长为
的长为  ;
; 的三边
的三边 ,
, ,
, 为边向外作正方形
为边向外作正方形 ,
, ,
, ,点
,点 ,
, ,
, 分别是这三个正方形的对角线交点,试分别利用
分别是这三个正方形的对角线交点,试分别利用 与
与 ,
, 与
与 之间的关系,运用旋转相似变换的知识说明线段
之间的关系,运用旋转相似变换的知识说明线段 与
与 之间的关系.
之间的关系.