题目内容
【题目】如图是以定长AB为直径的⊙O,CD为![]() 上的一条动弦(点C与A,点D与B不重合),CF⊥CD交AB于F,DE⊥CD交AB于E.
上的一条动弦(点C与A,点D与B不重合),CF⊥CD交AB于F,DE⊥CD交AB于E.
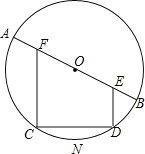
(1)求证:AF=BE;
(2)若弦CD的长度保持不变,四边形CDEF的面积是否也保持不变?并请说明理由.
【答案】(1)见解析;(2)四边形CDEF的面积保持不变.
【解析】
试题分析:(1)作OM⊥CD于M,根据垂径定理得到CM=DM,根据平行线等分线段定理证明结论;
(2)根据梯形中位线定理和梯形的面积公式解答即可.
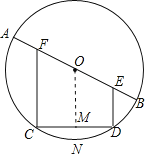
(1)证明:作OM⊥CD于M,
则CM=DM,
∵CF⊥CD,DE⊥CD,OM⊥CD,
∴CF∥OM∥DE,又CM=DM,
∴OF=OE,又OA=OB,
∴OA﹣OF=OB﹣OE,即AF=BE;
(2)∵弦CD的长度保持不变,
∴弦心距OM的长度保持不变,
由(1)得,OM是梯形CDEF的中位线,
∴OM=![]() (CF+DE),
(CF+DE),
∵四边形CDEF的面积=OM×CD,
∴四边形CDEF的面积保持不变.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目