题目内容
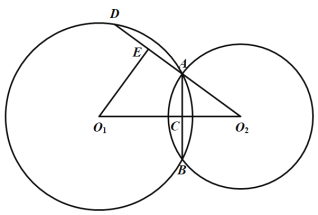
【题目】如图,⊙![]() 和⊙
和⊙![]() 相交于A、B两点,
相交于A、B两点,![]() 与AB交于点C,
与AB交于点C,![]() 的延长线交⊙
的延长线交⊙![]() 于点D,点E为AD的中点,AE=AC,联结
于点D,点E为AD的中点,AE=AC,联结![]() .
.
(1)求证:![]() ;
;
(2)如果![]() ,
,![]() ,求⊙
,求⊙![]() 的半径长.
的半径长.
【答案】(1)证明见解析;(2)5.
【解析】
(1)根据条件得到AC,AB的关系,再利用AC=AB即可解答.
(2)利用三角形相似即可解答.
⑴ ⊙O1和⊙O2相交于A、B两点,
∴O1O2是AB的垂直平分线
∴AB=2AC,
∵E为AD的中点
∴AD=2AE,O1E⊥AD,
∵AE=AC,
∴AB=AD,
∴O1E=O1C.
⑵ ∵O1E⊥AD,
∴∠O1EO2=90°,
在RT△O1EO2中,∠O1EO2=90°,O1O2=10,O1E=6,
∵O1E2+O2E2=O1O22,
O2E2=102-62=64,
∴O2E=8,
∵∠O1EO2=∠O2CA=90°,
∠O2=∠O2,
∴△O2EO1∽△O2CA,
∴![]() ,
,
∵O1O2=10,
AC=AE=O2E-O2A=8-O2A,O1E=6,
∴![]() ,
,
∴![]() A=5.
A=5.
即⊙![]() 的半径长为5.
的半径长为5.
故答案为5.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目