题目内容
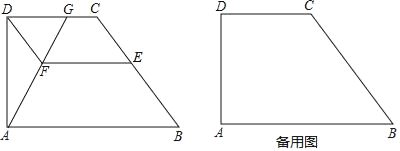
【题目】如图，已知AB∥CD，AC与BD相交于点E，点F在线段BC上，
，
．
(1)求证：AB∥EF；
(2)求S△ABE：S△EBC：S△ECD．
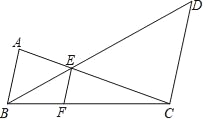
【答案】(1)证明见解析；(2)S△ABE：S△EBC：S△ECD＝1：2：4．
【解析】
（1）只要证明
＝
，即可推出EF∥CD解决问题；
（2）设△ABE的面积为m．利用相似三角形的性质，等高模型求出△BCE，△ECD的面积即可解决问题；
(1)∵AB∥CD，
∴
，
∵，
∴＝
，
∴EF∥CD，
∴AB∥EF．
(2)设△ABE的面积为m．
∵AB∥CD，
∴△ABE∽△CDE，
∴
＝(
)2＝
，
∴S△CDE＝4m，
∵
＝＝
，
∴S△BEC＝2m，
∴S△ABE：S△EBC：S△ECD＝m：2m：4m＝1：2：4．
练习册系列答案
相关题目
