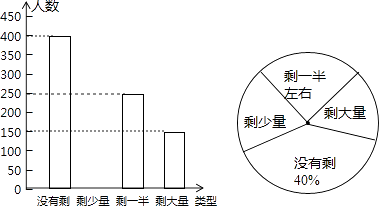
题目内容
【题目】如图，⊙O是△ABC的外接圆，AB是直径，作OD∥BC与过点A的切线交于点D，连接DC并延长交AB的延长线于点E．
（1）求证：DE是⊙O的切线；
（2）若AE=6，CE=2 
，求线段CE、BE与劣弧BC所围成的图形面积．（结果保留根号和π）
【答案】
（1）解：连结OC，如图，
∵AD为⊙O的切线，
∴AD⊥AB，
∴∠BAD=90°，
∵OD∥BC，
∴∠1=∠3，∠2=∠4，
∵OB=OC，
∴∠3=∠4，
∴∠1=∠2，
在△OCD和△OAD中，
，
∴△AOD≌△COD（SAS）；
∴∠OCD=∠OAD=90°，
∴OC⊥DE，
∴DE是⊙O的切线；
（2）解：设半径为r，则OE=AE﹣OA=6﹣r，OC=r，
在Rt△OCE中，∵OC2+CE2=OE2，
∴r2+（2 
）2=（6﹣r）2，解得r=2，
∵tan∠COE= 
= 
= ，
∴∠COE=60°，
∴S阴影部分=S△COE﹣S扇形BOC
= 
×2×2 ﹣ 
=2 ﹣ 
π．
【解析】（1）连结OC，根据切线的性质得∠BAD=90°，再根据平行线的性质，得到∠1=∠2，再由△AOD≌△COD，得到∠OCD=∠OAD=90°，即证得所求结论；
（2）设半径为r，在Rt△OCE中利用勾股定理得到r=2,再利用正切函数求出∠COE=60°，然后根据扇形面积公式和S阴影部分=S△COE-S扇形BOC进行计算即可得到BE与劣弧BC所围成的图形面积．
【考点精析】根据题目的已知条件，利用切线的判定定理和扇形面积计算公式的相关知识可以得到问题的答案，需要掌握切线的判定方法：经过半径外端并且垂直于这条半径的直线是圆的切线；在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）．
【题目】（1）填写下表,观察被开方数a的小数点与算术平方根
的小数点的移动规律：
a | 0.0016 | 0.16 | 16 | 1600 |
|
（2）根据你发现的规律填空：
①已知：
=2.683 ,
则
=_________, 
=________
②已知： 
=6.164，若
=61.64， 则x=____________,
（3）直接写出与a的大小.
