题目内容
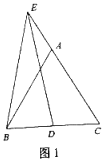
【题目】如图1,△ABC是等边三角形,点D是BC上一点,点E在CA的延长线上,连结EB、ED,且EB=ED.
(1)求证:∠DEC=∠ABE;
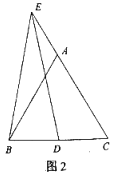
(2)点D关于直线EC的对称点为M,连接EM、BM:
①依题意将图2补全;
②求证:EB=BM.
【答案】(1)证明见解析;(2)①作图见解析;②证明见解析.
【解析】
(1)根据等边三角形的性质得到∠ABC=∠ACB=∠BAC=60°,再根据等边对等角以及三角形外角的性质即可得出结论;
(2)①根据题意作出图形即可;
②由轴对称的性质得到:DE=EM,DG=GM,再根据等腰三角形三线合一的性质得到∠2=∠1.由(1)的结论即可得到∠1=∠3.再证明△BEM是等边三角形即可得出结论.
(1)∵△ABC是等边三角形,∴∠ABC=∠ACB=∠BAC=60°.
∵BE=DE,∴∠EBD=∠EDB,∴∠EBA+∠ABC=∠CED+∠C,∴∠EBA =∠CED,即∠DEC=∠ABE;
(2)①作图如下:
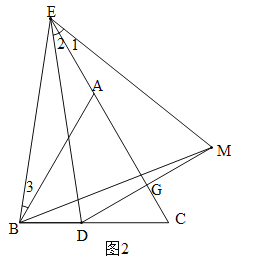
②∵D、M关于直线AC对称,∴DE=EM,DG=GM,∴∠2=∠1.由(1)得:∠2=∠3,∴∠1=∠3.
∵BE=DE,∴BE=ME.
∵∠3+∠BEA=∠BAC=60°,∴∠1+∠BEA=60°,∴∠BEM=60°.
∵BE=ME,∴△BEM是等边三角形,∴EB=BM.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
【题目】为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制成如下统计图表(单位:cm):
A | x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | x≥170 |
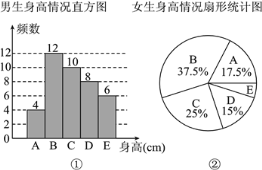
根据图表提供的信息,样本中,身高在160≤x<170之间的女生人数为( )
A. 8 B. 6 C. 14 D. 16