题目内容
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别是A(2,3)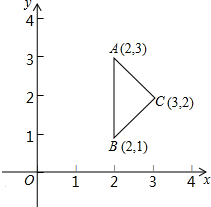 、B(2,1)、C(3,2).
、B(2,1)、C(3,2).
(1)判断△ABC的形状;
(2)如果将△ABC沿着边AC所在直线旋转一周,求所得旋转体的体积.
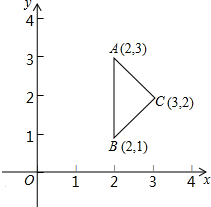 、B(2,1)、C(3,2).
、B(2,1)、C(3,2).(1)判断△ABC的形状;
(2)如果将△ABC沿着边AC所在直线旋转一周,求所得旋转体的体积.
(1)答:三角形是等腰直角三角形;
由A、B、C三点的坐标可知,
AC=
=
,
BC=
=
,
AB=3-1=2,
因为(
)2+(
)2=4=22,即AC2+BC2=AB2,AC=BC,
故此三角形是等腰直角三角形;
(2)圆锥的体积为
π•BC2•AC=
π×(
)2×
=
π.
由A、B、C三点的坐标可知,
AC=
| (2-3)2+(3-2)2 |
| 2 |
BC=
| (3-2)2+(2-1)2 |
| 2 |
AB=3-1=2,
因为(
| 2 |
| 2 |
故此三角形是等腰直角三角形;
(2)圆锥的体积为
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 2 |
| 2 |
| 3 |
| 2 |

练习册系列答案
相关题目

 D在BC上,连接BE,AD,AD的延长线交BE于点F.问AF与BE是否垂直?并说明理由.
D在BC上,连接BE,AD,AD的延长线交BE于点F.问AF与BE是否垂直?并说明理由.