题目内容
【题目】已知,点![]() 、
、![]() ,将线段
,将线段![]() 绕着原点
绕着原点![]() 逆时针方向旋转角度
逆时针方向旋转角度![]() 到
到![]() ,连接
,连接![]() ,将
,将![]() 绕着点
绕着点![]() 顺时针方向旋转角度
顺时针方向旋转角度![]() 至
至![]() ,连接
,连接![]() .
.
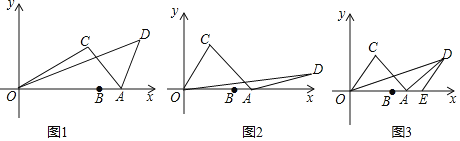
(1)当![]() ,
,![]() 时,求
时,求![]() 的长.
的长.
(2)当![]() ,
,![]() 时,求
时,求![]() 的长.
的长.
(3)已知![]() ,当
,当![]() 时,改变
时,改变![]() 的大小,求
的大小,求![]() 的最大值.
的最大值.
【答案】(1)10;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)将AO绕点A顺时针方向旋转60°至AN,连接AN,DN.通过SAS证明△AOC≌△AND,再证明∠OND=90°后利用勾股定理即可求解;
(2)将AO绕点A顺时针方向旋转120°至AN,连接AN,DN.通过SAS证明△AOC≌△AND,再证明∠OND=90°后利用勾股定理即可求解;
(3)将AO绕点A顺时针方向旋转90°至AN,可得点N为(8,8),利用两点距离公式求出NE的长,然后根据D在线段NE上时,DE最小为![]() ;D在线段NE的延长线上时DE最大为
;D在线段NE的延长线上时DE最大为![]() ,从而求出DE的最大值.
,从而求出DE的最大值.
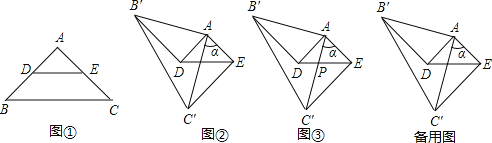
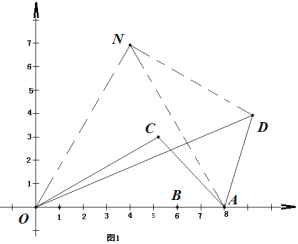
解:(1)如图1,将AO绕点A顺时针方向旋转60°至AN,连接AN,DN.
则△OAN是等边三角形.
∴ON=OA=AN=8.
∴∠OAN=∠ONA=∠CAD=60°.
∴∠OAN-∠NAC=∠CAD-∠NAC,即∠OAC=∠NAD.
在△AOC和△AND中
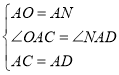 ,
,
∴△AOC≌△AND(SAS)
∴OC=ND,∠AND=∠AOC=30°.
又∵OB=6,
∴OC=ND=6.
∴∠OND=∠ONA+∠AND=90°.
∴![]() ;
;
(2)如图2,将AO绕点A顺时针方向旋转120°至AN,连接AN,DN,
∴△OAN是等腰三角形,
∵∠OAN=120°,
∴![]() ,∠AON=∠ANO=30°.
,∠AON=∠ANO=30°.
∵∠OAN=∠CAD=120°.
∴∠OAN-∠NAC=∠CAD-∠NAC,即∠OAC=∠NAD.
在△AOC和△AND中
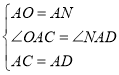 ,
,
∴△AOC≌△AND(SAS),
∴OC=ND,∠AND=∠AOC=60°.
∴∠OND=∠AND+∠ANO=90°,
又∵OB=6,
∴OC=OB=ND=6.
∴![]() ;
;
(3)如图3,将AO绕O顺时针旋转90°到AN,连接AN、DN、EN.
则N为(8,8),
则![]() .
.![]()
则(1)可得:△AOC≌△AND.
∴ND=OC=OB=6.
当D在线段NE上时,DE最小为![]() ;
;
当D在线段NE的延长线上时,DE最大为![]() .
.
即DE的最大值为![]() .
.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案