题目内容
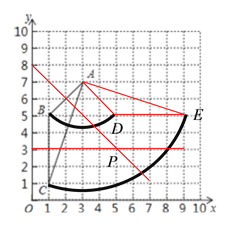
【题目】如图，在10×10的正方形网格中（每个小正方形的边长都为1个单位），△ABC的三个顶点都在格点上．建立如图所示的直角坐标系，
请在图中标出△ABC的外接圆的圆心P的位置，并填写： 圆心P的坐标：P（ , ）
（2）将△ABC绕点A逆时针旋转90°得到△ADE，画出图
形，并求△ABC扫过的图形的面积．
【答案】（1）P（ 5 ， 3 ） （2）
【解析】试题分析：
（1）由外心是三角形各边垂直平分线的交点可知，我们在方格纸中画出AB和BC两边的垂直平分线就可找到外心，并得到其坐标；
（2）如图，在旋转过程中，△ABC扫过的面积=S扇形ACE+S△ABC，因此我们只需要利用图中的信息由勾股定理计算出AC的长就可计算了.
试题解析：
（1）如图，利用图中的格点分别画出线段AB和BC的垂直平分线，两条垂直平分线的交点为所求的P点，由图可得点P的坐标为（5，3）；
（2）根据图中信息由勾股定理可得： 
，∴△ABC在旋转过程中扫过的面积为：S扇形ACE+S△ABC=
.
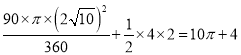练习册系列答案
开心试卷期末冲刺100分系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
