题目内容
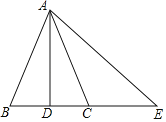
【题目】如图,在△ABC中,AB=AC,D是BC的中点,连接AD,E在BC的延长线上,连接AE,∠E=2∠CAD,下列结论:
①AD⊥BC;
②∠E=∠BAC;
③CE=2CD;
④AE=BE.
其中正确的个数是( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
等腰三角形的性质,“三线合一”,顶角的平分线,底边的高和底边上的中线,三条线互相重合便可推得.
解:①∵在△ABC中,AB=AC,D是BC的中点,
∴AD⊥BC;
②∵在△ABC中,AB=AC,D是BC的中点,
∴∠BAC=2∠CAD,
∵∠E=2∠CAD,
∴∠E=∠BAC;
③无法证明CE=2CD;
④∵在![]() 中,AB=AC,
中,AB=AC,
∴∠B=∠ACB,
∵∠ACB=∠E+∠CAE,∠E=∠BAC,
∴∠B=∠EAB,
∴AE=BE.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目