ЬтФПФкШн
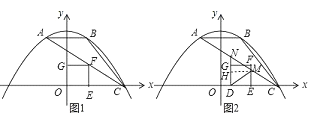
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНax2ЃЋbxЃЋcОЙ§ЁїABCЕФШ§ИіЖЅЕуЃЌгыyжсЯрНЛгк(0ЃЌ ![]() )ЃЌЕуAзјБъЮЊ(Ѓ1ЃЌ2)ЃЌЕуBЪЧЕуAЙигкyжсЕФЖдГЦЕуЃЌЕуCдкxжсЕФе§АыжсЩЯЃЎ
)ЃЌЕуAзјБъЮЊ(Ѓ1ЃЌ2)ЃЌЕуBЪЧЕуAЙигкyжсЕФЖдГЦЕуЃЌЕуCдкxжсЕФе§АыжсЩЯЃЎ
ЃЈ1ЃЉЧѓИУХзЮяЯпЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉЕуFЮЊЯпЖЮACЩЯвЛЖЏЕуЃЌЙ§ЕуFзїFEЁЭxжсЃЌFGЁЭyжсЃЌДЙзуЗжБ№ЮЊЕуEЃЌGЃЌЕБЫФБпаЮOEFGЮЊе§ЗНаЮЪБЃЌЧѓГіЕуFЕФзјБъЃЛ
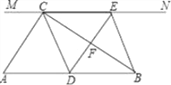
ЃЈ3ЃЉНЋЃЈ2ЃЉжаЕФе§ЗНаЮOEFGбиOCЯђгвЦНвЦЃЌМЧЦНвЦжаЕФе§ЗНаЮOEFGЮЊе§ЗНаЮDEFGЃЌЕБЕуEКЭЕуCжиКЯЪБЭЃжЙдЫЖЏЃЌЩшЦНвЦЕФОрРыЮЊtЃЌе§ЗНаЮЕФБпEFгыACНЛгкЕуMЃЌDGЫљдкЕФжБЯпгыACНЛгкЕуNЃЌСЌНгDMЃЌЪЧЗёДцдкетбљЕФtЃЌЪЙЁїDMNЪЧЕШбќШ§НЧаЮЃПШєДцдкЃЌЧѓtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
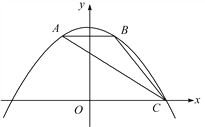
ЁОД№АИЁПЃЈ1ЃЉy=Љ![]() x2+
x2+![]() ЃЛЃЈ2ЃЉЃЈ1ЃЌ1ЃЉЃЛЃЈ3ЃЉЕБЁїDMNЪЧЕШбќШ§НЧаЮЪБЃЌtЕФжЕЮЊ
ЃЛЃЈ2ЃЉЃЈ1ЃЌ1ЃЉЃЛЃЈ3ЃЉЕБЁїDMNЪЧЕШбќШ§НЧаЮЪБЃЌtЕФжЕЮЊ![]() ЃЌ3Љ
ЃЌ3Љ![]() Лђ1ЃЎ
Лђ1ЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉвзЕУХзЮяЯпЕФЖЅЕуЮЊЃЈ0ЃЌ![]() ЃЉЃЌШЛКѓжЛашдЫгУД§ЖЈЯЕЪ§ЗЈЃЌОЭПЩЧѓГіХзЮяЯпЕФКЏЪ§ЙиЯЕБэДяЪНЃЛ
ЃЉЃЌШЛКѓжЛашдЫгУД§ЖЈЯЕЪ§ЗЈЃЌОЭПЩЧѓГіХзЮяЯпЕФКЏЪ§ЙиЯЕБэДяЪНЃЛ
ЃЈ2ЃЉЂйЕБЕуFдкЕквЛЯѓЯоЪБЃЌШчЭМ1ЃЌПЩЧѓГіЕуCЕФзјБъЃЌжБЯпACЕФНтЮіЪНЃЌЩше§ЗНаЮOEFGЕФБпГЄЮЊpЃЌдђFЃЈpЃЌpЃЉЃЌДњШыжБЯпACЕФНтЮіЪНЃЌОЭПЩЧѓГіЕуFЕФзјБъЃЛЂкЕБЕуFдкЕкЖўЯѓЯоЪБЃЌЭЌРэПЩЧѓГіЕуFЕФзјБъЃЌДЫЪБЕуFВЛдкЯпЖЮACЩЯЃЌЙЪЩсШЅЃЛ
ЃЈ3ЃЉЙ§ЕуMзїMHЁЭDNгкHЃЌШчЭМ2ЃЌгЩЬтПЩЕУ0ЁмtЁм2ЃЎШЛКѓжЛашгУtЕФЪНзгБэЪОDNЁЂDM2ЁЂMN2ЃЌЗжШ§жжЧщПіЃЈЂйDN=DMЃЌЂкND=NMЃЌЂлMN=MDЃЉЬжТлОЭПЩНтОіЮЪЬтЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЁпЕуBЪЧЕуAЙигкyжсЕФЖдГЦЕуЃЌ
ЁрХзЮяЯпЕФЖдГЦжсЮЊyжсЃЌ
ЁрХзЮяЯпЕФЖЅЕуЮЊЃЈ0ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЙЪХзЮяЯпЕФНтЮіЪНПЩЩшЮЊy=ax2+![]() ЃЎ
ЃЎ
ЁпAЃЈЉ1ЃЌ2ЃЉдкХзЮяЯпy=ax2+![]() ЩЯЃЌ
ЩЯЃЌ
Ёрa+![]() =2ЃЌ
=2ЃЌ
НтЕУa=Љ![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФКЏЪ§ЙиЯЕБэДяЪНЮЊy=Љ![]() x2+
x2+![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЂйЕБЕуFдкЕквЛЯѓЯоЪБЃЌШчЭМ1ЃЌ
Сюy=0ЕУЃЌЉ![]() x2+
x2+![]() =0ЃЌ
=0ЃЌ
НтЕУЃКx1=3ЃЌx2=Љ3ЃЌ
ЁрЕуCЕФзјБъЮЊЃЈ3ЃЌ0ЃЉЃЎ
ЩшжБЯпACЕФНтЮіЪНЮЊy=mx+nЃЌ
дђга![]() ЃЌ
ЃЌ
НтЕУ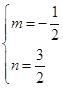 ЃЌ
ЃЌ
ЁржБЯпACЕФНтЮіЪНЮЊy=Љ![]() x+
x+![]() ЃЎ
ЃЎ
Щше§ЗНаЮOEFGЕФБпГЄЮЊpЃЌдђFЃЈpЃЌpЃЉЃЎ
ЁпЕуFЃЈpЃЌpЃЉдкжБЯпy=Љ![]() x+
x+![]() ЩЯЃЌ
ЩЯЃЌ
ЁрЉ![]() p+
p+![]() =pЃЌ
=pЃЌ
НтЕУp=1ЃЌ
ЁрЕуFЕФзјБъЮЊЃЈ1ЃЌ1ЃЉЃЎ
ЂкЕБЕуFдкЕкЖўЯѓЯоЪБЃЌ
ЭЌРэПЩЕУЃКЕуFЕФзјБъЮЊЃЈЉ3ЃЌ3ЃЉЃЌ
ДЫЪБЕуFВЛдкЯпЖЮACЩЯЃЌЙЪЩсШЅЃЎ
злЩЯЫљЪіЃКЕуFЕФзјБъЮЊЃЈ1ЃЌ1ЃЉЃЛ
ЃЈ3ЃЉЙ§ЕуMзїMHЁЭDNгкHЃЌШчЭМ2ЃЌ
дђOD=tЃЌOE=t+1ЃЎ
ЁпЕуEКЭЕуCжиКЯЪБЭЃжЙдЫЖЏЃЌЁр0ЁмtЁм2ЃЎ
ЕБx=tЪБЃЌy=Љ![]() t+
t+![]() ЃЌдђNЃЈtЃЌЉ
ЃЌдђNЃЈtЃЌЉ![]() t+
t+![]() ЃЉЃЌDN=Љ
ЃЉЃЌDN=Љ![]() t+
t+![]() ЃЎ
ЃЎ
ЕБx=t+1ЪБЃЌy=Љ![]() ЃЈt+1ЃЉ+
ЃЈt+1ЃЉ+![]() =Љ
=Љ![]() t+1ЃЌдђMЃЈt+1ЃЌЉ
t+1ЃЌдђMЃЈt+1ЃЌЉ![]() t+1ЃЉЃЌME=Љ
t+1ЃЉЃЌME=Љ![]() t+1ЃЎ
t+1ЃЎ
дкRtЁїDEMжаЃЌDM2=12+ЃЈЉ![]() t+1ЃЉ2=
t+1ЃЉ2=![]() t2Љt+2ЃЎ
t2Љt+2ЃЎ
дкRtЁїNHMжаЃЌMH=1ЃЌNH=ЃЈЉ![]() t+
t+![]() ЃЉЉЃЈЉ
ЃЉЉЃЈЉ![]() t+1ЃЉ=
t+1ЃЉ=![]() ЃЌ
ЃЌ
ЁрMN2=12+ЃЈ![]() ЃЉ2=
ЃЉ2=![]() ЃЎ
ЃЎ
ЂйЕБDN=DMЪБЃЌ
ЃЈЉ![]() t+
t+![]() ЃЉ2=
ЃЉ2=![]() t2Љt+2ЃЌ
t2Љt+2ЃЌ
НтЕУt=![]() ЃЛ
ЃЛ
ЂкЕБND=NMЪБЃЌ
Љ![]() t+
t+![]() =
=![]() ЃЌ
ЃЌ
НтЕУt=3Љ![]() ЃЛ
ЃЛ
ЂлЕБMN=MDЪБЃЌ
![]() =
=![]() t2Љt+2ЃЌ
t2Љt+2ЃЌ
НтЕУt1=1ЃЌt2=3ЃЎ
Ёп0ЁмtЁм2ЃЌЁрt=1ЃЎ
злЩЯЫљЪіЃКЕБЁїDMNЪЧЕШбќШ§НЧаЮЪБЃЌtЕФжЕЮЊ![]() ЃЌ3Љ
ЃЌ3Љ![]() Лђ1ЃЎ
Лђ1ЃЎ