题目内容
【题目】如图，已知正方形ABCD的边长为4，E是BC边上的一个动点，AE⊥EF，EF交DC于点F，设BE=x，FC=y，则当点E从点B运动到点C时，y关于x的函数图象是（ ）
A.
B.
C.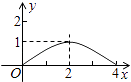
D.
【答案】C
【解析】解：∵AE⊥EF，∴∠AEB+∠FCE=90°
∵四边形ABCD是正方形，∴∠B=∠C=90° AB=BC=4，
∴∠BAE+∠AEB=90°，∴∠BAE=∠FCE，
∴△ABE∽△ECF，∴ 
，
∵BE=x，FC=y，∴EC=4﹣x，则有 
，
整理后得 y= 
x2+x 配方后得到y=﹣ 
（x﹣2）2+1
从而得到图象为抛物线，开口朝下，顶点坐标为（2，1）．
故选C．
【考点精析】通过灵活运用函数关系式和函数的图象，掌握用来表示函数关系的数学式子叫做函数解析式或函数关系式；函数的图像是由直角坐标系中的一系列点组成；图像上每一点坐标（x，y）代表了函数的一对对应值，他的横坐标x表示自变量的某个值，纵坐标y表示与它对应的函数值即可以解答此题．
新题型全程检测期末冲刺100分系列答案
【题目】某玩具厂生产一种玩具，本着控制固定成本，降价促销的原则，使生产的玩具能够全部售出．据市场调查，若按每个玩具280元销售时，每月可销售300个．若销售单价每降低1元，每月可多售出2个．据统计，每个玩具的固定成本Q（元）与月产销量y（个）满足如下关系：
月产销量y（个） | … | 160 | 200 | 240 | 300 | … |
每个玩具的固定成本Q（元） | … | 60 | 48 | 40 | 32 | … |
（1）每月产销量y（个）与销售单价x（元）之间的函数关系式为； 从上表可知，每个玩具的固定成本Q（元）与月产销量y（个）之间满足反比例函数关系式，求出Q与y之间的关系式；
（2）若每个玩具的固定成本为30元，求它的销售单价是多少元？
（3）若该厂这种玩具的月产销量不超过400个，求此时销售单价最低为多少元？
