��Ŀ����
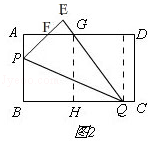
����Ŀ����ͼ����ʾ����֪�ھ���ABCD�У�AB=60cm��BC=90cm����P�ӵ�A��������3cm/s���ٶ���AB�˶���ͬʱ����Q�ӵ�B��������20cm/s���ٶ���BC�˶�������Q�����Cʱ��P��Q����ͬʱֹͣ�˶������P��Q�˶���ʱ��Ϊt��s����
��1����t=sʱ����BPQΪ���������Σ�
��2����BDƽ��PQʱ����t��ֵ��
��3����ͼ�ڣ�����BPQ��PQ�۵�����B�Ķ�Ӧ��ΪE��PE��QE�ֱ���AD���ڵ�F��G��
̽�����Ƿ����ʵ��t��ʹ��AF=EF��������ڣ����t��ֵ����������ڣ�˵�����ɣ�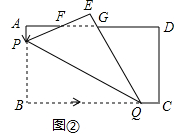
���𰸡�
��1��![]()
��2��
�⣺��ͼ1��
��P��PM��AD��
�� ![]() ��
��
�� ![]() ��
��
��PM=90�� ![]() t��
t��
��PN=NQ��PM=BQ��
��90�� ![]() t=20t��
t=20t��
��t= ![]() ��
��
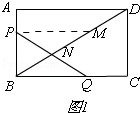
��3��
�⣺��ͼ2����GH��BQ��H��
��PB=PF=60��3t��
��AE=EF����AEP=��FEG����A=��F��
���AEP�ա�FEG��
��PE=EG��FG=AP��
��AG=PF=60��3t=BH��
��HQ=BQ��BH=20t����60��3t��=23t��60��
GQ=FQ��FG=BQ��AP=17t��
���ݹ��ɶ����ã�602=��17t��2����23t��60��2
��t1=4��t2=7.5���ᣩ��
��t=4
�����t=4��ʹAE=EF��
����������1���⣺��BP=BQʱ��60��3t=20t��
��t= ![]() ��
��
���Դ��ǣ� ![]() ��
��
�����㾫�������ڱ��⿼��ĵ��������ε����ʺ��ɶ����ĸ����Ҫ�˽���������ε���������ȣ���ƣ��ȱ߶ԵȽǣ���ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2���ܵó���ȷ�𰸣�

 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�